[PDF version of this document]|
[HV Home]
DEVS assignment
DEVS assignment
General Information
- The due date is Wednesday 3rd December 2002, before
23:55.
- Submissions must be done via WebCT.
Beware that WebCT's clock may differ slightly from yours.
As described on the Assignments page, all results
must be uploaded to WebCT and accessible from links in the
index.html file. There is no need to upload AToM3.
- The assignment can be made in groups of upto 2 people.
It is understood that all partners will understand the
complete assignment (and will be able to answer questions
about it).
- Grading will be done based on correctness and completeness
of the solution. Do not forget to document your requirements,
assumptions, design, simulation results, conclusions in detail !
- Extensions, if given, will involve extending not only the
alotted time, but also the assignment !
The problem
The purpose of this assignment is to model the behaviour of car
traffic on a straight stretch of road. This road is made up of
a sequence of small road segments.
Each road segment can hold only one car and is hence quite short
(typically 10m as we assume trucks are not allowed on this
stretch of road). If more than one car is present in a road segment, a
collision occurs.
The model will consist of a Coupled DEVS model named
RoadStretch. This model is made
up of of a concatenation of one Generator Atomic DEVS,
followed by a series of RoadSegment Atomic DEVS, and
terminated by a Collector Atomic DEVS as depicted
in Figure 1.
Figure 1: The Road Stretch
The following is a detailed description of the three different
Atomic DEVS as well as of the Car, Query
and QueryAck entities sent (as events)
between the Atomic DEVS building blocks.
Car
Cars are instances of the Car class and are generated
by the Generator Atomic DEVS, passed through the sequence
of RoadSegment Atomic DEVS, and finally end up at the
Collector Atomic DEVS.
The Car class is a container for all the relevant information
pertaining to a car.
A car has the following attributes set at instantiation time:
- v_pref: the car(driver)'s preferred speed.
Whenever adjusting its speed, the car will try to attain this speed.
This speed may not be attained in the current road segment due to
a speed limitation (v_max) of a road segment or due to
the inability to accelerate or decelerate too much in one road
segment.
The value of v_pref is, at instantiation time,
sampled from a uniform distribution over the range
[v_pref_min, v_pref_max[.
v_pref is a strictly positive real number as are
the lower and upper bounds. You should use Python's
random module which implements pseudo-random number
generators for various distributions.
- v_pref_min: lower bound on v_pref.
- v_pref_max: upper bound (not included
in the sampling interval) on v_pref.
- dv_pos_max: the car's maximum acceleration
(velocity increase), in one road segment. A positive number.
- dv_neg_max: the car's maximum deceleration
(velocity decrease), in one road segment. A positive number.
- departure_time: the time at which the car leaves
the Generator. It is the Generator's
responsibility to assign this value.
Note how, to keep things simple, dv_pos_max and
dv_neg_max are not sampled from a distribution
and will be the same for all cars. You are free to extend this
and use random values.
Note that if one wished to model the car driver's quality
of vision, one should add a parameter to the Car class
encoding this.
We give the Car class an attribute
distance_travelled which
changes during the course of the simulation to reflect its changing
state. The attribute distance_travelled is initialized (at
instantiation time) to 0. Each time a Car object leaves a road
segment, distance_travelled is incremented with L,
the length of that road segment (not all road segments need to have
the same length - note that in this assignment, all road segments do
have the same length of 10m so it would be possible to just
count the number of road segments traversed though that would not be
very general). Thus, at each point in simulated
time, distance_travelled will reflect the distance the car
has travelled, irrespective of the traffic system's topology.
A Car attribute v will keep track of the car's
current speed.
As shown in Figure 1, a Car instance is
output through a Generator's
car_out output port. It enters a RoadSegment
through that Atomic DEVS' car_in input port and leaves
again through that model's car_out output port.
Finally, the Car instance enters the Collector
Atomic DEVS through that model's car_in input port.
Query and QueryAck
The moment a car enters a new road segment, a Query
message (an instance of the Query class)
is sent to the next road segment through the sender road segment's
Q_send output port. The receiver road segment will
receive the query through its Q_recv input port.
This query is used to model, at a discrete event level of abstraction,
the driver's observation of the next road segment for the presence of
a car. In this discrete event model, where the road segments are the
"active" components (the road segments are modelled as DEVS',
not the cars, which are "passive"), the next road segment will,
after some observation delay observ_delay, reply
with a QueryAck message (an instance of the QueryAck
class) through its Q_sack "query send acknowledgement"
output port. The QueryAck message is received by the
Query's sender on the latter's Q_rack
"query receive acknowledgement" input port.
The Query class has no attributes. If the car driver's
vision were modelled, it might carry that information though.
The QueryAck class carries information back about the
presence of a car in the next road segment. It contains the single
attribute t_until_dep. This value indicates how
long it will take for the car (if present) to leave the next road
segment. The following values can be returned:
- 0 if there is no car present in the next road segment.
- A positive, non-zero number if there is a car present in the
next road segment. This value is calculated
as the length of the next road segment divided by the
speed of the car in that road segment at the time of the query.
Note that this is only an approximation. This makes sense as a human
observer can also only approximate the time it will take for the
car in the next road segment to leave that segment. Such an
approximation is called "dead reckoning": it is assumed that the
car in the next segment will maintain the same speed as at the time
of the observation. Note also how we are conservative and do not use
the remaining distance to be travelled in the next road segment but
rather the full length of the next road segment.
- A negative number (-1) to denote plus infinity.
This value will be returned if the car in the next segment
has velocity 0. This typically occurs when a collision has happened
and multiple cars pile up, all with velocity 0.
Generator
A Generator generates Car instances on its
car_out output port. The Inter Arrival Time (IAT) of
cars is uniformly distributed over the interval
[IAT_min, IAT_max].
A generator thus has the following parameters:
- IAT_min: IAT lower bound.
- IAT_max: IAT upper bound.
Note how a Generator has a Q_send output port
and a Q_rack input port exactly like a RoadSegment.
You may ignore this in your implementation.
In a more elaborate model however, the Generator would,
like a RoadSegment, look forward at the road segment ahead.
If a collision could occur (a car is present in the next segment and
the IAT is shorter than the time for that car to leave the next
segment), the generator will delay producing the next car's arrival.
Note how this strategy is also implemented in a GPSS GENERATE block.
It is the Generator's responsibility to:
- Assign the car's v_pref by sampling from a uniform
distribution over the range [v_pref_min, v_pref_max].
- Assign the car's dv_pos_max.
- Assign the car's dv_neg_max.
- Assign the car's departure_time:
the time at which the car leaves the Generator.
Note how a DEVS model has no access to a "global" time
(only the DEVS simulator keeps track of this). This global
time is needed to assign to departure_time.
You must thus add a state variable global_time
to the Generator and keep it properly updated
(in the internal transition function, using the IAT).
- Assign the car's initial velocity v.
There are several choices possible depending on what kind
of stretch of road we are modelling. If the arrival is from
the exit of a parking lot for example, it makes sense to give all
cars initial velocity v=0. If the arrival is from an
arbitrary traffic system, one may wish to sample the arrival
velocity from some distribution. Another approximation is to
let each car enter at its v_pref. Note how in the latter
case, it will never be possible for a car to travel faster than
its v_pref given the velocity adaptation scheme we use.
Collector
The Collector is where Cars leave the
system. Its main purpose is to collect statistics.
In this case, we are interested in two performance metrics:
- The transit_time of each car: the time between
departure from a Generator till the arrival in the
Collector. To be able to compute the transit_time
of each car, the Collector will take the difference between
the arrival time and the departure_time stored as
an attribute in the Car object.
Note how a DEVS model has no access to a "global" time
(only the DEVS simulator keeps track of this). This global
time is needed to know the arrival time of a car in the
Collector. You must thus add a state variable
global_time to the Collector and keep it properly
updated (in the external transition function, using the elapsed time).
- avg_v_pref_dev, the amount the average speed of each car
deviates from that car's preferred speed. Each car's preferred speed
is available as an attribute of that car object. The average speed
of a car is computed by dividing the car's attribute
distance_travelled by the car's transit_time.
Ideally, we would like as much insight as possible in the
distribution of the above performance metrics.
For simplicity, you should however not collect the distribution
in a table (as requested in class), but only the average
of these metrics.
Note how unlike a RoadSegment, a Collector
does not have a Q_recv input port nor a Q_sack
output port. This means that Query messages sent from
the last RoadSegment will not go anywhere and hence
that last RoadSegment will never receive a QueryAck.
This is reasonable as a Collector has an infinite capacity
for collecting cars. The fact that the last RoadSegment will
never receive a QueryAck is not a problem. A car entering
that last road segment will just continue at the
v_old velocity at which it entered the segment.
It is thus scheduled to leave that segment after
L / v_old.
RoadSegment
A road segment has the following parameters:
- L: the length of the road segment.
- v_max: the maximum allowed speed in the
road segment.
The maximum speed may be due to road conditions (potholes for example)
or due to speed limit road signs.
We assume cars will (try to) avoid speeding.
- observ_delay: the time it takes before
the road segment replies to a Q_send query message
received on its Q_recv input port. A reply comes in
the form of a QueryAck message through the road segment's
Q_sack "query send acknowledgement" output port.
The observ_delay models the observation delay and encodes
factors such as the visibility in the observed road segment.
Note that we are not modelling the quality of the car driver's
vision here. observ_delay is purely a property of a road
segment (and is not determined by a property of the car/driver).
The RoadSegment Atomic DEVS will have a list
cars_present as part of its state to keep track of
the cars currently in that road segment.
cars_present is initialized to [].
The moment a car enters a road segment (at velocity v_old,
found in the car's attribute v), that road segment
will first check if there are already cars present. If there are,
the arriving car will be added to the cars_present list,
and all cars' velocities v will be set to 0, denoting a collision.
If however, there are no cars present (the list of present cars
is empty), the RoadSegment immediately
sends a Query message to the model downstream, via the ouput
port Q_send.
It also schedules a departure of the car at time
L / v_old.
Note how there may only be one downstream model as otherwise there
would be a choice of where to go. This should be modelled explicitly
in a choice model.
Some elapsed time later, a QueryAck is received
interrupting the scheduled departure.
During that time, the car will have travelled a distance
xi = elapsed * v_old.
There still remains a distance remaining_x = L - xi
to be travelled to leave the road segment.
Usually, the delay (due to observation time of the next road segment)
is very short. If the road segment is connected to a
Collector however, a QueryAck will never be received
and the car will leave the road segment after the scheduled time
L / v_old.
When a QueryAck is received, the road segment's external
transition will handle it. It will update the distance still to be
travelled, and retrieve from the QueryAck object, the
t_until_dep of the car in the next road segment.
This time will be used locally as t_no_coll, the minimum time
the car must stay in the current road segment to not collide with
the car in the next road segment when leaving.
Note how collision may still occur as (1) the t_until_dep
received in the QueryAck is only an approximation and
(2) the car may not be able to slow down sufficiently within
the remaining distance in the current road segment.
Let's first consider the case where there is no car in the next
road segment and the t_until_dep received in the
QueryAck is thus 0.
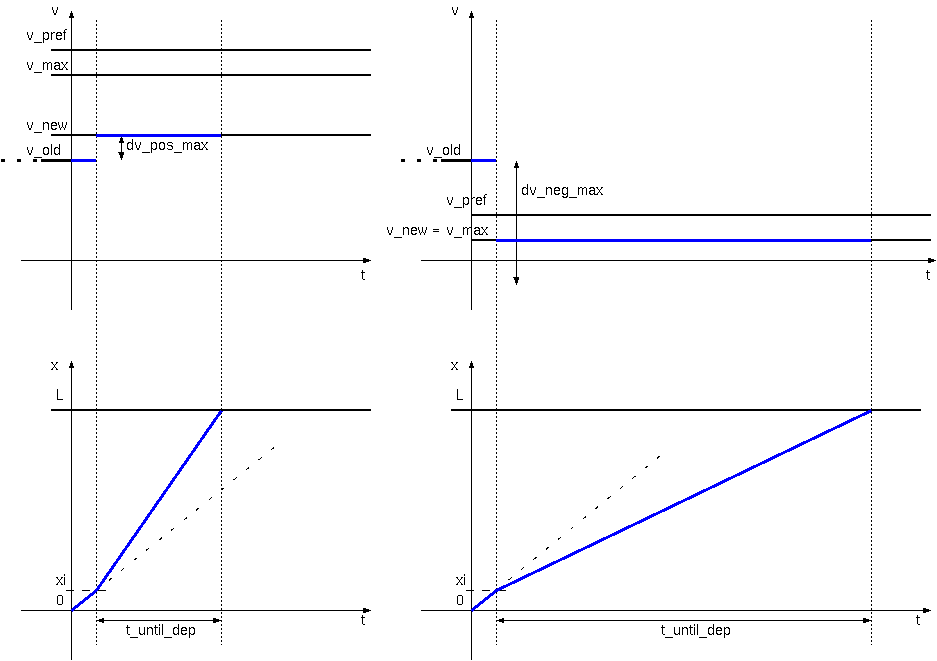
This case is depicted in Figure reffig:noCarBefore in two examples.
Figure 2: Adapting speed, no car in road segment ahead
As there are no restrictions on the speed imposed by the next
road segment, the car will want to update its speed to its
v_pref. However, the car should not exceed the
current road segment's speed limit v_max.
The new target speed is thus min(v_pref, v_max).
It may not be possible to attain this target speed due to
the maximum velocity changes dv_pos_max and
dv_neg_max. The final new speed v_new
will take this into account.
A departure is scheduled after t_until_dep = remaining_x / v_new.
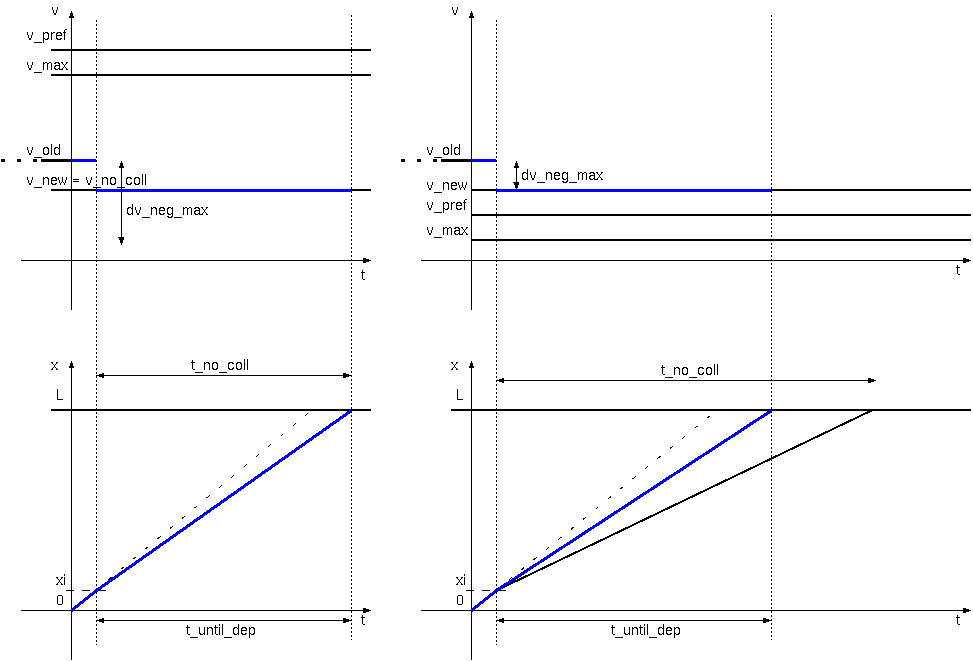
Let's now consider the case where there is a car in the next
road segment and the t_until_dep received in the
QueryAck is thus a positive number.
This case is depicted in Figure reffig:carBefore in two examples.
Figure 3: Adapting speed, car in road segment ahead
The special case of a negative number denoting plus infinity is
considered later.
Now, we cannot just set the target speed to min(v_pref, v_max)
as that might bring us to the next road segment too early
(i.e., before the car in that segment has left).
The time until departure must thus be
the maximum of t_no_coll (obtained from the
QueryAck's t_until_dep) and the time
it would take to leave at the intended target speed
remaining_x / min(v_pref, v_max).
This will require an updated speed of
remaining_x / max(t_no_coll, remaining_x / min(v_pref,
v_max)).
It may not be possible to reach this speed however due to
the maximum velocity changes dv_pos_max and
dv_neg_max. The final new speed v_new
will take this into account.
A departure is scheduled after t_until_dep = remaining_x / v_new.
If the car(s) in the next segment is/are standing still, as is
the case after a collision, or due to a v_max = 0,
a negative number (-1) will be returned as t_until_dep
in the QueryAck. This means that the target speed is
0. dv_neg_max will determine whether it is possible to
attain this speed. Note how there is nothing special about this case
(compared to the one where the t_until_dep returned
is a positive number).
Note how at any point during the t_until_dep,
the model might be interrupted by a Query from the previous
road segment (or generator) enquiring about the time until departure
of the car currently present (if any).
You must make sure to appropriately update t_until_dep
(remember how an external transition forgets about the remaining
time). You may either return in a QueryAck, a conservative
dead reckoning estimate L / v or a more accurate
estimate based on the updated t_until_dep.
Simulation
Perform a few simulation experiments.
Always choose the simulation duration sufficiently long enough to
get statistically relevant measurements.
Choose some meaningful values for the various parameters
to demonstrate the correctness of your model.
For example, make the behaviour deterministic so it is possible
to analytically determine the performance metrics.
Discuss your results !
Practical issues
You will use the PythonDEVS simulator found on the
MSDL DEVS page.
You need DEVS.py and Simulator.py.
Queue.py demonstrates how to model a cascade of processors
(of jobs) in PythonDEVS.
An older version of this example is given in a report.
The report gives background information on the
implementation of the DEVS simulator.
Note that in PythonDEVS, when an external transition is
triggered, this means that some external input has arrived on
one or more of the ports. Using peek, you can check
each of the ports for the presence as in
p = self.peek(self.IN1) in an external transition
function with a subsequent check if p == None: to determine
whether the received external input arrived on port self.IN1.
File translated from
TEX
by
TTH,
version 3.40 on 28 Nov 2003, 11:55.