

Next: 1.2 Basics of action
Up: 1 Introduction to Action
Previous: 1 Introduction to Action
As a starting point of action semantics, denotational semantics is studied very
thoroughly and has lots of applications. Its base, 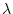 -calculus, is
accurate and rigorously defined. Because of this, models described in
denotational semantics can be easily analyzed.
-calculus, is
accurate and rigorously defined. Because of this, models described in
denotational semantics can be easily analyzed.
However, in the contemporary view of a modeler, the deficiency of denotational
semantics outweighs its merits. Its major drawback is the lack of modularity. In
a description, semantic definitions are globally visible. Part of the
description intertwines with another. When change has to be made, even if it is
only a minor change, it cannot be confined to a small area. People have to
propagate the change throughout the whole description. This process, of course,
is boring, time-consuming and error-prone.
This only addresses part of the problem. 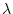 -notation is usually complex
and hardly read. For example, a simple statement ``A1 then A2" in action
semantics corresponds to the
-notation is usually complex
and hardly read. For example, a simple statement ``A1 then A2" in action
semantics corresponds to the 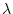 -notation
-notation
[Mos96]. This is good for computer processing, but not good for
humans. When reading this description, the programmer has to decipher the meaning of
the 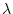 -notation, and reconstruct the underlying semantics. It turns out
that this reverse approach is extremely difficult; and any modification of the
description, which is based on this reverse process, is thus formidable.
-notation, and reconstruct the underlying semantics. It turns out
that this reverse approach is extremely difficult; and any modification of the
description, which is based on this reverse process, is thus formidable.


Next: 1.2 Basics of action
Up: 1 Introduction to Action
Previous: 1 Introduction to Action
Thomas Feng
2003-04-18
![]() -notation is usually complex
and hardly read. For example, a simple statement ``A1 then A2" in action
semantics corresponds to the
-notation is usually complex
and hardly read. For example, a simple statement ``A1 then A2" in action
semantics corresponds to the ![]() -notation
-notation