




Next: 2.4 Closure under Importation
Up: 2.3 Algorithms
Previous: 2.3.2 Alternate Algorithm for
Contents
Index
2.3.3 Importation
When model 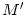 is imported into state
is imported into state 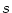 of model
of model 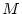 , a part of its
definition is merged with
, a part of its
definition is merged with 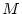 , while the rest is ignored. The
algorithm below describes this merging:
, while the rest is ignored. The
algorithm below describes this merging:
- As an stimulus of this importation, a
transition
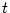 must be fired, or the submodel is placed in a
default state of the model so that it is required at the very
beginning of a simulation or execution.
must be fired, or the submodel is placed in a
default state of the model so that it is required at the very
beginning of a simulation or execution. 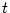 has the following
properties:
has the following
properties:
If such a transition is detected, the simulation/execution
environment must first prepare the substates of 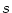 by importation
(since it is at that time a leaf state) before actually firing the
transition.
by importation
(since it is at that time a leaf state) before actually firing the
transition.
If an importation state is a default state of a model, the
simulation/execution environment must import the appropriate
submodel at the beginning. If the imported model requires more
submodels, they are also imported at that time. It is the
designer's responsibility to make sure that this repeated
importation process ends in finite and acceptable time.
- To import model
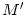 into importation state
into importation state 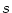 of
of 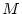 , the
following merging operations are performed:
, the
following merging operations are performed:
- The GUIDs of the states in
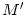 are modified to make them
globally unique within the states name space. This may be
implemented by adding a prefix. The
are modified to make them
globally unique within the states name space. This may be
implemented by adding a prefix. The 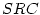 and
and 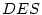 of each
transition are modified accordingly. The parent-children
relationship function
of each
transition are modified accordingly. The parent-children
relationship function 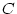 is modified accordingly.
is modified accordingly.
- The state hierarchy of
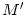 is merged with
is merged with 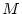 . All the
states in
. All the
states in 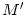 become substates of
become substates of 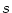 . The
. The 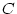 function of
function of
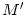 is combined with the
is combined with the 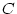 function of
function of 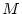 .
.
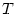 of
of 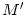 is merged with
is merged with 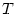 of
of 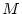 . If it is enforced
that the
. If it is enforced
that the 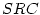 of any transition in
of any transition in 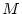 cannot be a state in
submodel
cannot be a state in
submodel 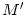 , the two transition sets do not have overlapping
elements. (However, the
, the two transition sets do not have overlapping
elements. (However, the 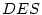 of some transitions may be
states in
of some transitions may be
states in 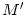 .) Note that the
.) Note that the 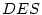 of a transition in
of a transition in 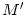 cannot refer to a state in
cannot refer to a state in 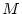 , since the simulation or
execution environment modifies it to be a unique GUID at the
time of importation.
, since the simulation or
execution environment modifies it to be a unique GUID at the
time of importation.
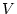 of
of 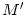 is merged with
is merged with 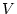 of
of 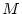 . If a variable in
. If a variable in
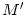 has the same name as a variable in
has the same name as a variable in 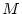 , it is considered
the same variable. If they have different types in a type
system, a run-time exception is raised.
, it is considered
the same variable. If they have different types in a type
system, a run-time exception is raised.
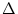 is merged after the GUIDs of states are changed.
is merged after the GUIDs of states are changed.
And the following properties of 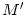 are ignored:
are ignored:
-
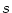 becomes a non-importation state,
because
becomes a non-importation state,
because 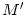 has already been imported into it.
has already been imported into it. 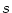 is no longer a
leaf state, either. When the importation is finished, there is no
knowledge of model
is no longer a
leaf state, either. When the importation is finished, there is no
knowledge of model 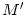 any more.
any more.
- Repeat steps 2.3.3 to 2.3.3 until no
importation state
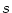 is found in the path from
is found in the path from 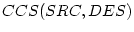 to
to
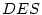 or
or 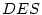 itself.
itself.
After this merging of one or more submodels, transition 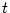 can be
fired according to any of the algorithms described in previous
sections.
can be
fired according to any of the algorithms described in previous
sections.





Next: 2.4 Closure under Importation
Up: 2.3 Algorithms
Previous: 2.3.2 Alternate Algorithm for
Contents
Index
Thomas Huining Feng
2004-04-28
![]() is imported into state
is imported into state ![]() of model
of model ![]() , a part of its
definition is merged with
, a part of its
definition is merged with ![]() , while the rest is ignored. The
algorithm below describes this merging:
, while the rest is ignored. The
algorithm below describes this merging:
![]() by importation
(since it is at that time a leaf state) before actually firing the
transition.
by importation
(since it is at that time a leaf state) before actually firing the
transition.
![]() are ignored:
are ignored:
![]() can be
fired according to any of the algorithms described in previous
sections.
can be
fired according to any of the algorithms described in previous
sections.