|
To specify a system as a model in a formalism, the two important parts of the formalism must be well-understood by all the designers and whoever wants to reuse parts of the system: the syntax and the semantics. The syntax enforces certain rules on every model designed in the formalism, while the semantics defines the concrete meaning of every model that conforms to the syntax. If the formalism is executable, its semantics provides the basis for simulation and execution; if the formalism is non-executable, its semantics helps ensure a unique interpretation of a model among multiple designers and users.
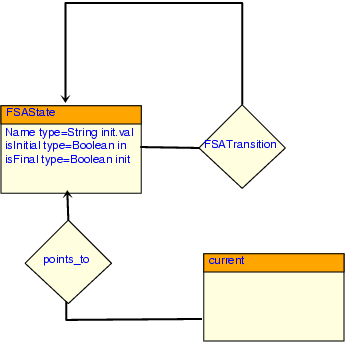
The formalism, if it is considered as a model itself, can be explicitly modeled with another formalism. In this case, the formalism to be modeled is called a meta-model. There are many benefits to meta-modeling. One of those is that the syntax of the modeled formalism can be very concisely and explicitly defined. For example, the syntax of FSA (Finite State Automata) can be easily modeled by an ER (Entity-Relationship) diagram as shown in Figure 1.1. This syntactic definition is much more rigorous than a definition in a natural language. A parser can be built from it, which automatically checks whether a model is an FSA.
Another benefit is that a user can easily design his/her own formalism
that best fits a specific application area. With a tool capable of
generating a modeling environment from a meta-model, such as AToM![]() (A Tool for Multi-formalism and Meta-Modeling) developed in the MSDL
(Modeling, Simulation and Design Lab) of McGill University
[1] [2], the designer gets a
domain-specific modeling environment. The environment is then used to
solve problems specific to the application domain. Model designers can
thus make full use of their knowledge in that
domain. [3]
(A Tool for Multi-formalism and Meta-Modeling) developed in the MSDL
(Modeling, Simulation and Design Lab) of McGill University
[1] [2], the designer gets a
domain-specific modeling environment. The environment is then used to
solve problems specific to the application domain. Model designers can
thus make full use of their knowledge in that
domain. [3]