5.5.2 Compound Statements

Figure 5.1: An invalid DCharts model that contains compound statements in the output

Figure 5.2: A DCharts model that contains simple statements in the output

Because of the restriction of actions in DCharts models, compound statements cannot be directly written in the action list of the output of a transition. Suppose comp_stm1, comp_stm2, ... are compound statements, and simp_stm1, simp_stm2, ... are simple statements. The model in Figure 5.1 is invalid since the output of a transition is a list of compound statements instead of simple statements. On the contrary, the model in Figure 5.2 is valid.

It is important to transform a model with compound statements in its output into a valid form, since the statements discussed later are mostly compound statements. This transformation can always be found with the following method. (Since the composition of compound statements is still a compound statement, this method only consider transitions that have a single compound statement in their output.)

1. A GUID is assigned to each compound statement. It is assumed that there is no event with the same name as the GUID in the model. If there is an event whose name conflicts with a GUID, simply add an implementation-dependent prefix to all the GUIDs.

2. Create a top-level orthogonal component.

3. Suppose the compound statement contains the following substatements: $stm_1$, $stm_2$, ..., $stm_n$. There are such substates in the orthogonal component: $s_0$ (default state), $s_1$, $s_2$, ..., $s_n$.

4. Transition from $s_0$ to $s_1$ reacts to the GUID of the compound statement (as an event name) and executes $stm_1$ in the output. It generates a unique event $e_1$ with the parameters that it receives. The transition from $s_1$ to $s_2$ reacts to event $e_1$ and executes $stm_2$. It generates a unique event $e_2$ with the same parameters. Transition from $s_2$ to $s_3$ reacts to event $e_2$ and executes $stm_3$. It generates a unique event $e_3$ with the same parameters. ... Transition from $s_{n-1}$ to $s_n$ reacts to event $e_{n-1}$ and executes $stm_n$. It generates a unique event $e_n$ with the same parameters. Transition from $s_n$ to $s_0$ reacts to event $e_n$ and generates ``return GUID'' as an event.

5. For each transition $t$ from $SRC$ to $DES$ with this compound statement as its $\lambda$, a new state $s$ is added.

6. The original transition is replaced by two new transitions. The transition from $SRC$ to $s$ is the same as $t$, except that its $DES$ is $s$, and its $\lambda$ is an action that generates the GUID of the compound statement as an event. The parameters of this new transition become the parameters of the generated event. That event triggers the transition from $s_0$ to $s_1$ in the orthogonal component.

7. A transition is created from $s$ to $DES$ reacting to the ``return GUID'' event.

8. Repeat the above steps wherever a compound statement is found in the output, until all the output actions become simple statements or lists of simple statements (separated by a comma).

Figure 5.3: An example of the transformation from a compound statement in the output into simple statements

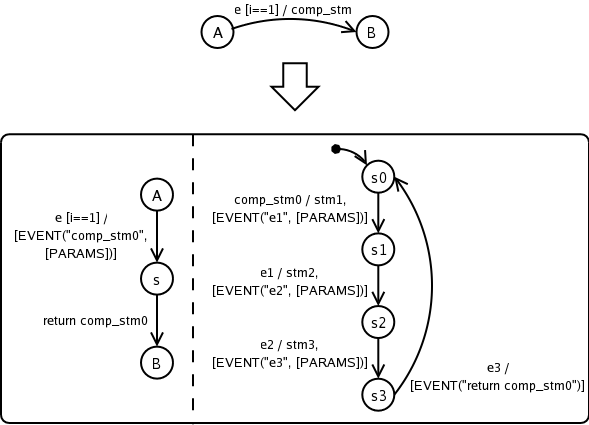
As an example, Figure 5.3 shows the transformation from a model with a compound statement in its output into a valid DCharts model. It assumes comp_stm to be a compound statement consisting of stm1, stm2 and stm3, which may be simple statements or compound statements. The model in the upper part is converted into the model in the lower part. If stm1, stm2 or stm3 is not a simple statement or a list of simple statements, this transformation is repeated.

As a result of this transformation, the output of each transition becomes a simple statement or a list of simple statements. (Note that this transformation may be done with graph grammars [33].)

Sequential execution of substatements in the compound statement is guaranteed by this transformation. However, synchronization is lost. Actions in other orthogonal components may be executed during the execution of those substatements, and the execution result of those interleaving actions becomes unpredictable. This semantics is different from executing a compound statement in a critical session provided by the simulator or executor. To solve this problem, it is suggested that the simulator or executor provide actions that allow designers to control the critical sessions. If such actions are available, the orthogonal component generated by this transformation is explicitly placed in a critical session. All the statements in it are executed continuously without interleaving with other actions. This topic is out of the scope of this thesis.