DEVS Flattening with muModelica and pyDEVS

Team

Jesse Doherty

260182547

Motivation

The semantics of DEVS were originaly described for atomic DEVS, and it was shown that coupled DEVS could be flattened into atomic DEVS. This means that any DEVS simulator only needs to simulate atomic DEVS. However, simulators will instead simulate full coupled DEVS. This is done probably to maintain the original model structure when simulating.

Having the simulator capable of simulating full coupled DEVS is useful because it allows the simulator to take advantage of some optimizations, such as parallelization. These optimizations are part of the simulator itself, but it might be useful to have optimizations performed on the actual model. It could also be useful to be able to analyze the model to check properties or help optimization. Having our models as coupled DEVS would make this more difficult, since the structure is more complex. Instead this analysis and optimization should be performed on a flattened version of the model, to allow simpler implementation.

Proposal/Requirements

We propose to implement a version of the DEVS flattening procedure to create a coupled to atomic DEVS compiler. This compiler will be done using the muModelica Modelica compiler with the DEVS compiler addition and will output pyDEVS code. This system will hopefully allow for analysis of the atomic models.

Design/Models

Version 1 (uncompleted)

This version was started to overcome some of the difficulties of dealing with the muModelica AST structure. The flattening procedure was implemented directly in the pyDevs printing code. As the compiler produced pyDevs code for a given coupled DEVS unit, a flattened version would also be produced.

This design was deficient in two regards. First it did not expose any of the DEVS structure to the compiler. This removed the possibility of performing analysis in the compiler. The second deficiency was that the flattening procedure was very simple. A flattened coupled model would simply contain instances of each atomic sub-model in the original model, and instances of flattened models for each coupled sub-model. This is a problem because it makes analysis of the generated code more difficult.

This version was abandoned for a more complex design, but is still partially present in the devsmc.py file.

Version 2

This version intended to expose more of DEVS structure to the compiler. It was also intended to perform more inlining of the flattened structure.

To allow more of the DEVS structure to be exposed to the compiler, new classes were created to capture the structure. This classes are in structure to the Modelica DEVS classes used by muModelica DEVS extension. The class hierarchy can be seen in the following diagram

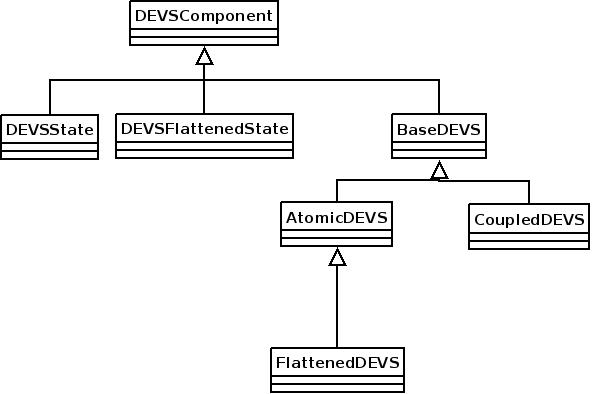
The flattened version of state and DEVS were created to facilitate flattening. As each coupled DEVS is flattened, a DEVSFlattenedState and a FlattenedDEVS instance is created.

Basic design

For each coupled DEVS in the original model, the flattener outputs a flattened version. These flattened versions are not interdependent, though they are dependent on the atomic DEVS that are part of the coupled structure.

The flattening is split into several logical phases.

Detailed design
Collecting models

The models are collected from the original modelica file using a simple AST visitor DevsCollector. It traverses the AST and finds class definitions. If the class is a DEVS class, it appends it to either a list of atomics, a list of coupled models, or a list of states.

Connecting the DEVS structure

Once a DEVS object is created to represent the component in the compiler, the AST structure for that component is passed to another visitor(DevsClassCollector) to collect useful information for that component. From this information the models can be linked to their states, and states to their models; and component members can be added to the object. These components include submodels, inputs, outputs, and connections. In addition, connections are stored in a structure of python dictionaries and lists to allow easy access to influencee information.

Topological ordering

Coupled DEVS form a directed acyclic graph of component type dependency with their sub-model structure. From this we can compute a topological ordering. This ordering is necessary when processing a coupled component with coupled sub-components. If the sub components have not been processed, then the higher level component cannot be processed.

Flattening

Each coupled DEVS is flattened in reverse topological order.

First empty objects are created for the flat state and model. Then contents are added to the state and model. The contents of the state consist of records of what atomic components are required for the flat model. This is done by adding all atomic sub-components of the model and recording their name. Then for each coupled sub-component, the components from flat versions of the sub-component are added with updated names. These names are simply the original nameswith the name of the sub-component and _ prepended.

Once members are added, the connections must be flattened. The idea behind the connection flattening is to connect the atomics directly. When a coupled model is involved in the connection, then all atomics involved that coupled model's port internal connections are connected to the other end of the connection being flattened.

With the coupled model flattened, the code gen needs to be able to create an __init__ for the flattened model. This is done by including the __init__ from coupled sub-models with a renaming similar to the renaming done for states. These init methods are recorded and updated to use the new state members.

Printing

Printing is done by the FlattenedDEVS class. First the init method is generated, then the timeAdvance, a method for getting the immediate action, a method getting port connection if an atomic is an influencee of another, the intTransition, and output methods. The extTransition is not currently implemented.

The timeAdvance method will go through each member of the flat model, and checking its timeAdvance (Note: each member of the flat model is an Atomic model at this point). The minimum is found and returned.

The getIStar method is used to find the next component to perform an internal transition. This is done by finding the first component with a ta that matches the timeAdvance of this model.

The isInfluencees method does a lookup in the dictionary structure storing connections for the flat model. If the model is influenced then a list of tuples of in/out ports is returned.

The intTransition method will first execute the intTransition of the immediate component. Then it checks each other component, if its a influencee, an external transition is performed for it, otherwise its elapsed time is incremented.

The output method will go through all the ports of the immediate component that are connected to one of the self ports, and poke the output to the correct port.

Implementation

The Flattening procedure is implemented in python, and uses the muModelica compiler with DEVS extension.

The files are available here

Experiments

The flattening procedure was applied to the queue.mo example in queueInModelica directory of examples in the provided zip file. Relevant files are in muModelica/devs/flatten/ The results are as follows. 

class Root( AtomicDEVS ):
  def __init__( self, pqs, name ):
    self.state = RootState()
    self.state.p2 = Processor(name=p2, qn=pqs)
    self.state.p3 = Processor(name=p3, qn=pqs)
    self.state.p1 = Processor(name=p1, qn=pqs)
    self.state.generator = Generator(name=generator, ia=pia, ib=pib, szl=psa, szh=psb)

  def timeAdvance( self ):
    ta = self.state.p2.timeAdvance()
    minT = ta - self.state.p2_e
    return minT    ta = self.state.p3.timeAdvance()
    tmpT = ta - self.state.p3_e
    if tmpT < minT:
      minT = tmpT
    return minT    ta = self.state.p1.timeAdvance()
    tmpT = ta - self.state.p1_e
    if tmpT < minT:
      minT = tmpT
    return minT    ta = self.state.generator.timeAdvance()
    tmpT = ta - self.state.generator_e
    if tmpT < minT:
      minT = tmpT
    return minT
  def getIStar( self ):
    ta = self.timeAdvance()
    aTa = self.state.p2.timeAdvance()
    sig = aTa - self.state.p2_e
    if sig == ta:
      return self.state.p2
    aTa = self.state.p3.timeAdvance()
    sig = aTa - self.state.p3_e
    if sig == ta:
      return self.state.p3
    aTa = self.state.p1.timeAdvance()
    sig = aTa - self.state.p1_e
    if sig == ta:
      return self.state.p1
    aTa = self.state.generator.timeAdvance()
    sig = aTa - self.state.generator_e
    if sig == ta:
      return self.state.generator

  def isInfluencees( self, ir, ie ):
    if i == self.state.p2:
      ports = []
      if j == self.state.p3:
        ports.append((self.state.p2.discard,self.state.p3.inport))
      if j == self:
        ports.append((self.state.p2.out,self.out))
      return ports
    if i == self.state.p3:
      ports = []
      if j == self:
        ports.append((self.state.p3.out,self.out))
        ports.append((self.state.p3.discard,self.discard))
      return ports
    if i == self.state.p1:
      ports = []
      if j == self.state.p2:
        ports.append((self.state.p1.discard,self.state.p2.inport))
      if j == self:
        ports.append((self.state.p1.out,self.out))
      return ports
    if i == self.state.generator:
      ports = []
      if j == self.state.p1:
        ports.append((self.state.generator.out,self.state.p1.inport))
      return ports
    return None

  def intTransition( self ):
    iStar = self.getIStar()
    iStar.outputFnc()
    iStar.intTransition()
    ta = self.timeAdvance()
    if self.state.p2 == iStar:
      self.state.p2_e = 0.0
    else:
      self.state.p2_e += ta
      infl = self.isInfluencees(iStar, self.state.p2)
      if infl != None:
        for (lp, rp) in infl:
          self.state.p2.poke(rp, iStar.peek(lp))
        self.state.p2.elapsed = ta + self.state.p2_e
        self.state.p2.extTransition()
        self.state.p2_e = 0.0
    if self.state.p3 == iStar:
      self.state.p3_e = 0.0
    else:
      self.state.p3_e += ta
      infl = self.isInfluencees(iStar, self.state.p3)
      if infl != None:
        for (lp, rp) in infl:
          self.state.p3.poke(rp, iStar.peek(lp))
        self.state.p3.elapsed = ta + self.state.p3_e
        self.state.p3.extTransition()
        self.state.p3_e = 0.0
    if self.state.p1 == iStar:
      self.state.p1_e = 0.0
    else:
      self.state.p1_e += ta
      infl = self.isInfluencees(iStar, self.state.p1)
      if infl != None:
        for (lp, rp) in infl:
          self.state.p1.poke(rp, iStar.peek(lp))
        self.state.p1.elapsed = ta + self.state.p1_e
        self.state.p1.extTransition()
        self.state.p1_e = 0.0
    if self.state.generator == iStar:
      self.state.generator_e = 0.0
    else:
      self.state.generator_e += ta
      infl = self.isInfluencees(iStar, self.state.generator)
      if infl != None:
        for (lp, rp) in infl:
          self.state.generator.poke(rp, iStar.peek(lp))
        self.state.generator.elapsed = ta + self.state.generator_e
        self.state.generator.extTransition()
        self.state.generator_e = 0.0
    return self.state

  def output( self ):
    iStar = self.getIStar()
    infl = self.isInfluencees(iStar, self)
    if infl != None:
      for (lp, rp) in infl:
        self.poke(rp, iStar.peek(lp))

You can see each of the output methods as described previously. One thing to note is the lack of loops for most operations. Instead each component is dealt with individually, as though the loop were unrolled.

Conclusions

This implementation has provided a high level representation of DEVS structure in the muModelica compiler. It uses this structure to then produce a flat version of each coupled component provided to it. This version is still dependent on Atomic models, but acts itself as an atomic DEVS and is not dependent on any coupled components or other flattened components. The code produced is very inlined, except for calls to atomics and the __init__ methods. It even produces code which resembles unrolled loop code. This is hoped to allow some more analysis and optimization of the code at the python level.

References

Presentation

My presentation is available here