Introduction

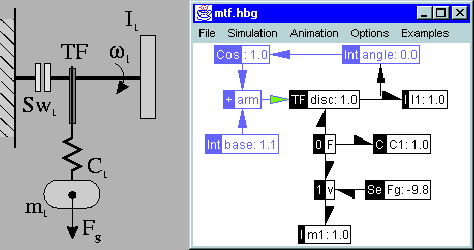
Bond graphs [Karnopp, Margolis, & Rosenberg1990,Paynter1961] are an elegant and powerful formalism to model the continuous behavior of physical systems based on energy exchange. Signals that represent variables with no energy content modulate energy flows. Mathematical operations on these signal values can be executed by block diagram components. To illustrate, consider the rotational mechanics system and its corresponding bond graph in Fig. 1 where energy components are shown in black whereas the signal components are shown in gray. A mass m₁ is attached to a rotating disc by a rope with elasticity C₁. The disc rotates about a rod with inertia I₁. Since the rod is not centered on the disc, gravitational force acting on the mass m₁ causes a torque as a function of rotation angle. The modulation of force by the angle is represented by the modulated TF component in the bond graph. The modulation ratio (arm in the bond graph in Fig. 1) depends on the angle, which is computed by integrating the angular velocity in the Int component. Arm is a sinusoidal function of this angle, modeled by the Cos component and used to modulate the TF. A small base value prevents the value of arm from becoming negative or 0.

  

Figure 1: A rotational mechanics bond graph example.

There is a growing interest in the bond graph community to model hybrid systems that combine continuous behavior with discrete mode transitions, e.g., [Breedveld1996,Mosterman & Biswas1998,Strömberg, Top, & Söderman1993]. This allows the model designer to focus on system behavior at a desired level of temporal and spatial detail, while abstracting more detailed phonemena into instantaneous, discrete, changes.

HYBRSIM³ is a modeling and simulation environment that supports the hybrid bond graph modeling paradigm [Mosterman1997,Mosterman & Biswas1998]. Hybrid bond graphs extend the basic continuous bond graph formalism with a primitive discontinuous switching mechanism controlled by finite state machines [Kohavi1978]. A critical characteristic of hybrid system models is that they may cause changes in causality (e.g., a diode either enforces voltage or current, depending on its mode of operation). HYBRSIM does not generate a global system of equations, but instead at each integration step propagates known variable values (input and state values) throughout the model. A causal analysis after discrete switchings determines which bond graph components are state variables in the new configuration and also whether sufficient known values exist (viz., whether the number of equations and unknowns corresponds) to continue the simulation process.

The advantage of this approach lies in the flexible treatment of systems where the system state vector may change and causal relations among variables may change with discrete switchings. When the system model is represented as a global DAE, a consistent mapping between state vector variable values before and after the discrete switch is required. Because all components in HYBRSIM keep the values of their variables locally, no explicit mapping is required. After the discrete structural changes have converged, an iteration procedure based on the physical principle of conservation of state [Mosterman & Biswas1997a] is applied that updates the continuous state variable values to consistent values.