


Next: A Consistent Projection
Up: Problem Analysis
Previous: Conservation of State
Before the derivation of the conservation equations, we first
study the behavior of system variables across discontinuities. The
set of system variables can be decomposed into those that appear
differentiated, x, and those that only appear algebraically, y.
When discontinuities occur, jumps in
the state variables x cause impulses on the rate variables
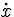 due to the derivative nature, which may propagate along
algebraic variables, y, and ultimately back to interact with
other
due to the derivative nature, which may propagate along
algebraic variables, y, and ultimately back to interact with
other 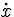 variables.
Impulses between rate variables have to satisfy the conservation
constraint. For example, the two capacitor system can be described
by Eq. (1) where
variables.
Impulses between rate variables have to satisfy the conservation
constraint. For example, the two capacitor system can be described
by Eq. (1) where
![\begin{displaymath}
x =
\left[\begin{array}
{c}
v_1 \\ v_2\end{array}\right];
y =
\left[\begin{array}
{c}
i\end{array}\right]\end{displaymath}](img10.gif)
When the switch is closed and v1 and v2 have values inconsistent
with v1 = v2, impulses occur based
on the v1 = v2 and C1 (v1+ - v1-) = -C2 (v2+ - v2-)
constraints. The latter can be derived from Eq. (1) by
first eliminating y from all equations with x to yield
![\begin{displaymath}
\left[\begin{array}
{cc}
C_1 & C_2 \\ C_1 & C_2\end{array}\r...
...}\right]
\left[\begin{array}
{c}
v_1 \\ v_2 \end{array}\right].\end{displaymath}](img11.gif)
This is a system of dependent equations. Eliminating one and integrating
the remaining equation results in
![\begin{displaymath}
\left[\begin{array}
{cc}
C_1 & C_2 \\ \end{array}\right]
\in...
...[\begin{array}
{c}
\dot{v_1} \\ \dot{v_2}\end{array}\right]
= 0\end{displaymath}](img12.gif)
or,
![\begin{displaymath}
\left[\begin{array}
{cc}
C_1 & C_2 \\ \end{array}\right]
\le...
...array}
{c}
v_1^+ - v_1^- \\ v_2^+ - v_2^-\end{array}\right]
= 0\end{displaymath}](img13.gif)
The constraint that the capacitor voltages are equal when the switch
is closed can be expressed as
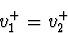
and combined with Eq. (6) v1+ and v2+ can be
derived.
In this example, impulses occur on all 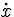 and
y variables. If this is
not the case,
and
y variables. If this is
not the case, 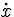 can be split into variables
can be split into variables 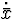 that cause
impulses because of discontinuities in
that cause
impulses because of discontinuities in 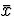 and variables
and variables 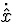 that do not because of continuous
behavior of
that do not because of continuous
behavior of 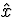 .
Note that the continuous character causes the latter to have the convenient
property
.
Note that the continuous character causes the latter to have the convenient
property
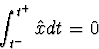
as well as (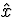 is continuous)
is continuous)
![\begin{displaymath}
\int_{t^-}^{t^+} \dot{\hat{x}} dt = [\hat{x}]_{t^-}^{t^+} = 0\end{displaymath}](img20.gif)
Also, 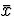 may have a step discontinuity at t but no impulse, and,
therefore, the integral over an infinitesimal interval is as well,
may have a step discontinuity at t but no impulse, and,
therefore, the integral over an infinitesimal interval is as well,
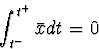
These properties are used to derive a general methodology for finding the
conservation constraints from a given matrix DAE.



Next: A Consistent Projection
Up: Problem Analysis
Previous: Conservation of State
Pieter J. Mosterman ER
7/27/1998
![\begin{displaymath}
x =
\left[\begin{array}
{c}
v_1 \\ v_2\end{array}\right];
y =
\left[\begin{array}
{c}
i\end{array}\right]\end{displaymath}](img10.gif)
![\begin{displaymath}
\left[\begin{array}
{cc}
C_1 & C_2 \\ C_1 & C_2\end{array}\r...
...}\right]
\left[\begin{array}
{c}
v_1 \\ v_2 \end{array}\right].\end{displaymath}](img11.gif)
![\begin{displaymath}
\left[\begin{array}
{cc}
C_1 & C_2 \\ \end{array}\right]
\in...
...[\begin{array}
{c}
\dot{v_1} \\ \dot{v_2}\end{array}\right]
= 0\end{displaymath}](img12.gif)
![\begin{displaymath}
\left[\begin{array}
{cc}
C_1 & C_2 \\ \end{array}\right]
\le...
...array}
{c}
v_1^+ - v_1^- \\ v_2^+ - v_2^-\end{array}\right]
= 0\end{displaymath}](img13.gif)