Transients generated by failures are dynamic, therefore,
the signatures of
the observed variables change over time. For example, a variable may
have a magnitude reported normal
and a 
derivative
which is above normal. Over time the variable value will
go above normal. Incorporating effects of
higher order derivatives in the comparison process is referred to as
progressive monitoring.
It replaces derivatives that do not match the observed
value with the value of derivatives of
one order higher in the signature.
Fig. 12 shows time stamps marked 1, 2, and
3, where a lower order effect is replaced by manifested higher order
effects. If the predicted deviation of higher order derivatives
do not match the observed value, the fault is rejected.
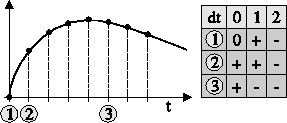
Figure 12: Dynamic behavior of higher order derivatives.
Progressive monitoring is activated
when there is a discrepancy between a predicted value and
a monitored value that deviates
(this applies to 
and higher order
derivatives). At every time point, it is
checked whether the next higher derivative could make
the prediction consistent with the observation. If this
next higher derivative value is normal the next
higher derivative value is considered, until there is either a conflict in
prediction and observation, a confirmation, or an unknown
value is found.
To illustrate, Fig. 13 shows the predicted and monitored
behavior for a sudden increase in outflow resistance
in the bi-tank system in Fig. 4,
where -1, 0, 1 maps onto low, normal, high and a period indicates
that the value is unknown.
The two observed variables are the outflow of the left tank,
, and the pressure in the right tank, 
. Not all monitoring output
is shown; the boxes depict the monitored values at time steps where the
set of hypothesized faults changes or where the tracking of an
observation's transient behavior is terminated.
The actual observations and the newly inferred set of possible faults and
their signatures are listed. The values on the top of each box
represent the measured signal magnitude ( order), slope
( derivative), and 
derivative
expressed in qualitative terms.
Below the reported measurements are the predicted signatures
of the measured variables for each hypothesized fault.
Consider fault 
and measurement in Fig. 13.
At step 9, the reported
value for is still normal (its value has not exceeded the error
threshold), and this agrees with the signature 0,0,1 for . At
step 23, the reported value for is 1,0 (magnitude above
normal), which no longer appears to be consistent with fault 's
signature. However, when progressive monitoring is applied,
the derivative, which is positive, makes an impact on both the
derivative and magnitude of the signal, and the prediction
for is changed to 1,1,1. Updating the
prediction in this manner keeps the signature consistent with
the observation, and
is still considered a viable fault hypothesis.
Hypothesized faults are dropped if their signatures do not
match observations for a sufficient number of steps.
Note that in step 23 the slope for is reported to be 0 whereas the
magnitude deviates. This is an artifact of our implementation.
The deviation in a slope is computed from the first
set of observations after an initial magnitude deviation is detected.
Therefore, the initial magnitude deviation may be detected before a slope
deviation is detected.
Figure 13: Progressive monitoring for fault .