Physical systems are by nature continuous, but often exhibit nonlinearities that make behavior generation complex and hard to analyze especially with qualitative reasoning schemes. This complexity is often reduced by linearizing model constraints so that component models (e.g., transistors, oscillators) exhibit multiple piecewise linear behavior or by abstracting time so that component models (e.g., switches, valves) exhibit abrupt discontinuous behavior changes[2, 11]. In either case, the physical components are modeled to operate in multiple modes, and system models exhibit mixed continuous/discontinuous behaviors.
Typically, simulation methods for generating physical system behavior, whether quantitative (e.g., [12]) or qualitative (e.g., [5, 8]) impose the conservation of energy principle and continuity constraints to ensure that generated behaviors are meaningful. Energy distribution among the elements of the system defines system state, and energy distribution over time reflects the history of system behavior.
Bond graphs[12] provide a general methodology for
modeling physical systems in a domain independent way. Its
primary elements are two energy storage elements or buffers, called
capacitors and inductors,
and a third element,
the resistor, which dissipates energy to the
environment[10, 12]. Two other
elements, sources of flow and effort, allow transfer of energy
between the system and its environment.
In addition, the modeling
framework provides idealized junctions that connect sets of
elements and allow lossless transfer of energy between them.
Two other specialized junctions, transformers and gyrators,
allow conversion of energy from one form to another. The use of the bond
graph modeling language in building compositional models of complex
systems has been described elsewhere[1].
State changes in a system are caused by energy exchange among its components, which is expressed as power, the time derivative, or flow, of energy. Power is defined as a product of two conjugate power variables: effort and flow. Given conservation of energy holds for a system, the time integral relation between energy variables and power variables implies continuity of power, and, therefore, effort and flow. As discussed earlier, discontinuities in behavior are attributed to time scale abstraction and parameter abstraction.
Consider an example of an ideal non-elastic collision in
Fig. 1. A bullet of mass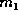 
and velocity 
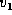hits an
unattached piece of wood of mass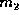 
, initially at rest.
The collision causes the bullet to get implanted in the wood,
forming one body of mass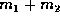 
moving with velocity say 
.
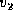The initial situation is represented as two bond graph fragments.
Each fragment has an inertial element (mass) connected by a 1-junction
to a zero effort source (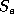 
) which indicates that there are no forces
acting on either the bullet or the wood. Because there are no
sources, the momentum after collision is conserved,
so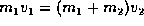 
, i.e.,
.
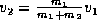A closer look at the model structure reveals that the initially independent masses become dependent at the instant of collision by virtue of a 0-junction connection, with no dissipation or energy storage elements involved. This represents a discontinuous change in the model, attributed to the modeling assumption that the collision is ideal and non-elastic. A more complete model of the situation would include dissipative and stiffness effects, and the two buffer velocities could not change instantaneously. If the goal of behavior generation is simply to determine the trajectory and final velocity of the bullet-wood system, the more abstract model allowing an abrupt change in velocity is reasonable and computationally efficient.
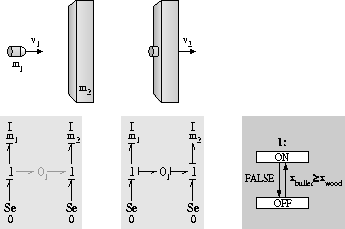
Figure 1: Hybrid Model: Ideal non-elastic collision of two
masses.
Our previous work[9, 10] in developing a uniform approach to analyzing mixed continuous/discontinuous system behavior without violating fundamental physical principles such as conservation of energy and momentum, led to the development of a hybrid modeling and behavior analysis scheme that combines