1.2.1 Finite State Automata

The syntax of the FSA formalism is defined by means of meta-model in Figure 1.1. An FSA consists of states and transitions between states. A state has three properties:

• Name, a string that denotes the unique ID of a state.

• isInitial, a boolean that decides whether a state is the initial state. There must be exactly one initial state in each FSA model.

• isFinal, a boolean that decides whether a state is a final state. There must be at least one final state in each FSA model.

A transition, when triggered, changes the model from one state (source state) to another (destination state). (The destination state may be the same as the source state.) In the ER meta-model, a transition is represented as a relation between states.

Input symbol is a property of transitions, which is not visible from the graphical representation of the meta-model. It defines a single symbol that triggers the transition. When that symbol is received and the model is in the source state of a transition (the starting of the arc), the transition is triggered, and the model changes to the new state (the ending of the arc with an arrow).

The input symbols are taken one by one from an input sequence. If there is no enabled transition (a transition is enabled if and only if the model is in its source state and the current input is its input symbol) for one of the symbols, an error is raised, and the FSA halts. This error means the FSA does not accept such an input sequence, or more formally, the language (the set of accepted input sequences) defined by the FSA does not include such a sentence (one single input sequence ended with an end mark).

The FSA formalism also requires that when an accepted input sequence ends, the FSA must be in one of the final states. Otherwise, the input sequence is not accepted.

Figure 1.6: A simple FSA example

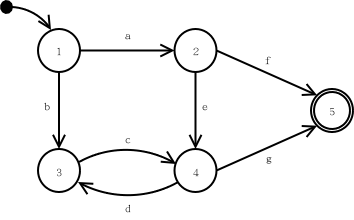
A simple FSA example is shown in Figure 1.6. Its initial state is state 1 (a state with a black dot pointing to it). Its final state is state 5 (a state with a double-line border). This FSA accepts the language:

$$\{af, ae(dc)^*g, b(cd)^*cg\}$$

As a result, af, aedcg, aedcdcg, bcg, bcdcg are all accepted sentences, while a, aedg and bcd are unaccepted.