As a typical example of hybrid systems, consider the evaporator vessel
in Fig. 1 that is part of the secondary cooling system
in a fast breeder nuclear
reactor [5]. In this system,
a sodium pump maintains a sufficient flow of coolant in the loop.
To keep the level of fluid in the evaporator vessel from
going over a prespecified maximum, an overflow mechanism is activated
to drain excessive fluid once this level is reached. The flow of
liquid through the overflow pipe builds up momentum, and the
evaporator behavior can be described by the level of fluid in the
evaporator, L, and the fluid momentum, p.
A detailed continuous phase space diagram
is shown on the left in Fig. 2 for a given inflow.
It exhaustively depicts
how relevant system variables relate to each other.
The system tends to a steady state, and highly nonlinear
but continuous
behavior may occur near the overflow level because of adhesive forces
in the fluid, the intake area of the overflow, and the fluid
surface area. If the detailed effects are abstracted away, the overflow
mechanism can be modeled to create a model configuration change
between two distinct modes where (1) the fluid level is below the
overflow level, and (2) the fluid level is above the overflow
level. Phase space behavior is piecewise linear, shown on the right in
Fig. 2, and switching occurs at ![]() which is called
the switching surface.
We refer to this form of model
abstraction as a parameter abstraction [6].
which is called
the switching surface.
We refer to this form of model
abstraction as a parameter abstraction [6].
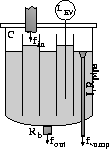
Figure 1: A hydraulics system with two distinct modes of operation.
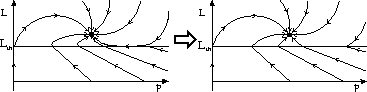
Figure 2: Phase space of evaporator
behavior. The
right-hand phase space description abstracts away small parameters
effects near the threshold in the left-hand phase space.
Time scale abstraction does not abstract away physical
parameters, but collapses time so that the effects of fast change
appear to be instantaneous and discontinuous [6].
An example of this is given by the
bouncing ball in Fig. 3. In case of an elastic collision, the
ball moves towards the switching surface ![]() with negative
velocity,
with negative
velocity, ![]() . When this point is reached, the kinetic energy
of the ball is stored in the form of elastic energy in the ball, which
is then turned back into kinetic energy as the ball uncompresses and
reverses
. When this point is reached, the kinetic energy
of the ball is stored in the form of elastic energy in the ball, which
is then turned back into kinetic energy as the ball uncompresses and
reverses ![]() in a very short interval of time. Phase space
behavior is shown in Fig. 4. In case the velocity
reversal occurs on a time scale much smaller than the time scale at
which overall behavior occurs, the continuous nonlinear phase space
behavior on the left can be modeled as an instantaneous jump in
in a very short interval of time. Phase space
behavior is shown in Fig. 4. In case the velocity
reversal occurs on a time scale much smaller than the time scale at
which overall behavior occurs, the continuous nonlinear phase space
behavior on the left can be modeled as an instantaneous jump in
![]() upon collision, shown on the right by double arrow heads.
In summary, hybrid systems operate in piecewise continuous phase
spaces, where governing equations change at switching surfaces,
possibly accompanied by jumps in state variables.
upon collision, shown on the right by double arrow heads.
In summary, hybrid systems operate in piecewise continuous phase
spaces, where governing equations change at switching surfaces,
possibly accompanied by jumps in state variables.
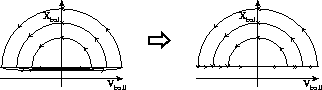
Figure 4: Phase space of a bouncing ball.
The velocity reversal
in a very short period of time in the left-hand phase space is
abstracted into instantaneous transitions on the right.
Behaviors of systems that exhibit multiple modes are best represented by an integrated formalism that represents behaviors in the distinct modes of operation using continuous models, specified as fields in phase space. Discrete mode switches occur at disctinct points in time to switch the active mode resulting in a new field description for continuous behavior generation. Fields are often defined by systems of linear and nonlinear ordinary differential equations [4], and numerical simulation methods may be employed to solve these equations. Similarly, a number of approaches with well defined execution semantics, such as Petri nets and finite state automata, have been applied to discrete system modeling [1].
Many numerical methods rely on the continuity assumptions in the
dynamic system models. Near the discontinuous boundary, a wide
variety of behaviors may occur. Following the classification
in [11], Fig. 5
categorizes three types of behaviors in phase space
according to the directions of
vector-field normal components in modes ![]() and
and ![]() ,
,
![]() and
and ![]() .
The simulation may make a large error when a
surface is crossed and a mode switch is detected. This is shown in
Fig. 6 on the left. To minimize these errors, the simulation
time step may have to be reduced to determine precisely where the mode
switch occurs. Adopting a variable step approach greatly reduces the
simulation error.
.
The simulation may make a large error when a
surface is crossed and a mode switch is detected. This is shown in
Fig. 6 on the left. To minimize these errors, the simulation
time step may have to be reduced to determine precisely where the mode
switch occurs. Adopting a variable step approach greatly reduces the
simulation error.
Using a variable step size works well in many cases, but it may result in problems when chattering along a switching surface occurs (Fig. 7). These chattering motions may be intentionally designed in sliding mode behavior, such as in anti-lock braking systems [8, 9]. Chattering occurs when the field vectors are directed towards the switching surface as shown in Fig. 5. During sliding mode operation, the system switches between modes at the switching surface at a very fast rate, producing a fast chattering behavior motion. This causes the aggregate behavior along the switching surface to progress very slowly and simulated time almost comes to a halt. This slow component of the dynamics along the sliding surface has to be approximated either by equivalence in control [12] or equivalence in dynamics [3] so that a larger step size could be used by an integration scheme without introducing untolerable errors.
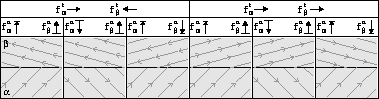
Figure 5: Types of phase space behaviors near a switching surface.
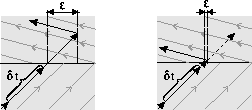
Figure 6: Error of a fixed step (left) and variable step (right)
integration at a switching surface.
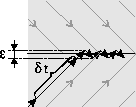
Figure 7: A hybrid system may chatter.