When a discrepancy between measurement and nominal value is detected,
a backward propagation
algorithm operates on the temporal causal graph to implicate component
parameters.
Implicated component parameters are labeled - (below normal)
and + (above normal). The algorithm propagates deviant
values backward on the directed arcs
and consistent 
deviation labels are assigned sequentially
to vertices along the path if they do not have a previously
assigned value.
An example is shown in Fig. 3 for a deviant right tank
pressure 
in the bi-tank system (Fig. 1).
initiates back propagation
along 
and implicates 
below normal ( 
) or 
above normal ( 
). The next step along
implicates 
, and
implicates 
, and so on.
The algorithm operates depth-first along instantaneous edges, and
is terminated along a path when a conflicting
assignment is reached. All component parameters along this
path are possible faults.
Backward propagation does not terminate
at normal measurements, for reasons discussed in detail
elsewhere [6, 8].
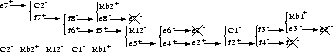
Figure 3: Backward propagation to find faults.