Let I be a discrete indexing set and 
,
, be a continuous, 
,
flow on a possibly open subset 
of 
, called a chart
(Fig 2a) [2].
The sub-domain of where
a continuous flow in time occurs is called a patch,
.
The flows constitute the piecewise
continuous part of the hybrid system.
Points within the system are specified by 
, a
location in chart 
at time t.
An explicitly defined isolated
point that does not embody continuous behavior is called a
pinnacle, 
.
The discrete switching function 
is defined as a
threshold function on . If 
then the system transitions from chart to 
,
defined by the mapping 
.
The piecewise continuous
level curves 
are denoted as 
,
and define patch boundaries. If a flow
includes the level curve, , it
contains the boundary point, 
(see Fig 2a).
In summary, a hybrid dynamic system is defined
by the 5-tuple
(1) 
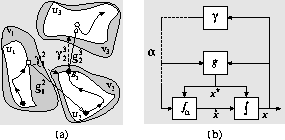
Figure 2: Hybrid dynamic systems.
Trajectories in the system start at an initial point
and if 
,
,
the point flows in 
as specified by 
until the minimal time 
at which
for some 
.
Computing
the transformation 
takes the trajectory from 
to
.
The point
is regarded as a new initial point. In case
the trajectory is immediately
transferred to
.
Fig. 2b shows a schematic representation
of this semantics and a sequence of transitions is of the form
