Hybrid systems combine piecewise continuous behavior with discrete transitions. Hybrid dynamic systems extend this behavior with the notion of time to model the behavior of dynamic physical systems. Physical systems obey the principles of conservation of energy and continuity of power, and combine phenomena that occur at different time scales (i.e., fast and slow). At any specified level of interest, continuous system behavior can be abstracted, so that behavior appears to have discontinuous changes that intersperse modes of continuous behavior. Mode changes occur when system variables cross threshold values, and state events or external control events occur.
Fig. 1 illustrates that a hybrid system operates on a
domain with discrete, 
, and continuous,
dimensions. Behavior in this space is specified by
a piecewise continuous domain, V, that specifies
variable flow, 
, uniquely on the time-line.
Hybrid dynamic system behavior evolves
over time, has an established direction of flow, and must necessarily
cover the complete interval on the time-line for which it is
specified. Therefore, the piecewise
continuous intervals in temporal behavior evolution are
adjacent to each other with no gaps (see Fig. 1).
Piecewise continuous interval behavior
is represented by well behaved, continuous
functions f, called fields, which may be linear or nonlinear,
and often specified by a set of nonlinear ordinary differential
equations [2]. An instance of temporal behavior
in a field is called a flow, 
.
Switching from one flow to another occurs
at well-defined points in time
when system variable values reach or exceed prespecified
threshold values.
This defines an interval-point paradigm where flows
are piecewise continuous and any discontinuous
changes that occur have to be simple [7], i.e.,
limit values exist at points of discrete switching.
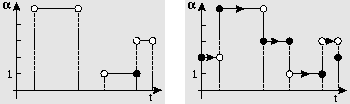
Figure 1: A hybrid system (left) and a hybrid dynamic system (right).