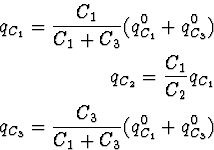Next: Modulated Impulsive Forces
Up: Examples
Previous: Local Conservation
In case of explicitly modeled interaction with the system environment,
conservation principles may be violated. Consider the electrical circuit
in Fig. 6 which has a modulated voltage source VR, i.e.,
the voltage drop across R is enforced on C2. The system
of equations can be compiled as
![\begin{displaymath}
\left.\begin{array}
{c}
\left[\begin{array}
{cccccc}
C_1 & 0...
...} \\ {i}_{C_2} \\ {i}_{C_3}\end{array}\right]\end{array}\right.\end{displaymath}](img71.gif)
In this system, the first three rows contain the
equations that model the constituent
time-derivative behavior of the three capacitors, C1, C2, and
C3, and, therefore, are part of f. So,
![\begin{displaymath}
\dot{\bar{x}} =
\left[\begin{array}
{c}
\dot{v}_{C_1} \\ \do...
...egin{array}
{c}
v_{C_1} \\ v_{C_2} \\ v_{C_3}\end{array}\right]\end{displaymath}](img72.gif)
The equation on the fourth row represents the
nodal equation summing the currents of C1, C3, and
R to . The last two rows contain
equations that represent the algebraic constraints
vC3 = vC1 and vC2 = vC1 (due to the
modulated source, VR), respectively.
The equations on the last three rows
constitute h, and the last two of them
have no algebraic variables so they are part of 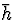 .The remaining equation in h yields
.The remaining equation in h yields
![\begin{displaymath}
\hat{y} =
\left[\begin{array}
{c}
i_{C_1} \\ i_{C_3}\end{array}\right]\end{displaymath}](img73.gif)
and, therefore,
![\begin{displaymath}
\tilde{y} =
\left[\begin{array}
{c}
i_{C_2}\end{array}\right].\end{displaymath}](img74.gif)
Figure 6:
Explicit interaction with the environment.
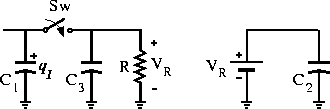 |
This results in the matrix partitioning
![\begin{displaymath}
F' =
\left[\begin{array}
{cc}
1 & 0 \\ 0 & 0 \\ 0 & 1\end{a...
...& 0 & 0 \\ 0 & C_2 & 0 & 1 \\ 0 & 0 & C_3 & 0\end{array}\right]\end{displaymath}](img76.gif)
and
![\begin{displaymath}
\hat{H}' =
\left[\begin{array}
{cc}
-1 & -1\end{array}\righ...
...[\begin{array}
{cccc}
\frac{1}{R} & 0 & 0 & 0\end{array}\right]\end{displaymath}](img77.gif)
Now, the pseude-inverse of F' is
![\begin{displaymath}
F'^+ =
\left[\begin{array}
{ccc}
1 & 0 & 0 \\ 0 & 0 & 1\end{array}\right]\end{displaymath}](img78.gif)
and
![\begin{displaymath}
\hat{H}' F'^+ F'' =
\left[\begin{array}
{cccc}
-C_1 & 0 & -C_3 & 0\end{array}\right]\end{displaymath}](img79.gif)
which yields the conservation equations
![\begin{displaymath}
\left[\begin{array}
{cccc}
\frac{1}{R} & 0 & 0 & 0\end{array...
...\ \dot{v}_{C_2} \\ \dot{v}_{C_3} \\ {i}_{C_2}\end{array}\right]\end{displaymath}](img80.gif)
Integrating the conservation equations gives the projection direction
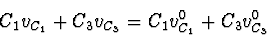
which, combined with the differentiated equations
![\begin{displaymath}
\left[\begin{array}
{ccc}
1 & -1 & 0 \\ 1 & 0 & -1 \\ \end{a...
...ray}\right]
=
\left[\begin{array}
{c}
0 \\ 0\end{array}\right],\end{displaymath}](img82.gif)
constitutes a system of equations of rank three with three variables.
The solution in terms of the conserved quantity, charge (q = C v),
is
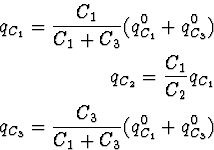
which shows that the charge on C1 and C3 is conserved, but
there may be an instantaneous change of charge on C2. This is
conform the model, which shows explicit interaction with the
environment between C2 and the battery VR.
Note that the current of C2, iC2, cannot be solved in
terms of differentiated variables. To find the value of this
variable, all 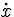 have to be eliminated from its equation.
The result is an algebraic relation that poses no additional
constraints on the dynamic, differential equation, behavior of
the system. The only additional information is about
system variable values (e.g., required for graphing purposes).
have to be eliminated from its equation.
The result is an algebraic relation that poses no additional
constraints on the dynamic, differential equation, behavior of
the system. The only additional information is about
system variable values (e.g., required for graphing purposes).



Next: Modulated Impulsive Forces
Up: Examples
Previous: Local Conservation
Pieter J. Mosterman ER
7/27/1998
![\begin{displaymath}
\left.\begin{array}
{c}
\left[\begin{array}
{cccccc}
C_1 & 0...
...} \\ {i}_{C_2} \\ {i}_{C_3}\end{array}\right]\end{array}\right.\end{displaymath}](img71.gif)
![\begin{displaymath}
\dot{\bar{x}} =
\left[\begin{array}
{c}
\dot{v}_{C_1} \\ \do...
...egin{array}
{c}
v_{C_1} \\ v_{C_2} \\ v_{C_3}\end{array}\right]\end{displaymath}](img72.gif)
![\begin{displaymath}
\hat{y} =
\left[\begin{array}
{c}
i_{C_1} \\ i_{C_3}\end{array}\right]\end{displaymath}](img73.gif)
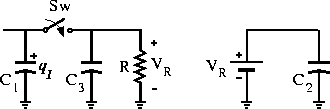
![\begin{displaymath}
F' =
\left[\begin{array}
{cc}
1 & 0 \\ 0 & 0 \\ 0 & 1\end{a...
...& 0 & 0 \\ 0 & C_2 & 0 & 1 \\ 0 & 0 & C_3 & 0\end{array}\right]\end{displaymath}](img76.gif)
![\begin{displaymath}
F'^+ =
\left[\begin{array}
{ccc}
1 & 0 & 0 \\ 0 & 0 & 1\end{array}\right]\end{displaymath}](img78.gif)
![\begin{displaymath}
\left[\begin{array}
{cccc}
\frac{1}{R} & 0 & 0 & 0\end{array...
...\ \dot{v}_{C_2} \\ \dot{v}_{C_3} \\ {i}_{C_2}\end{array}\right]\end{displaymath}](img80.gif)
![\begin{displaymath}
\left[\begin{array}
{ccc}
1 & -1 & 0 \\ 1 & 0 & -1 \\ \end{a...
...ray}\right]
=
\left[\begin{array}
{c}
0 \\ 0\end{array}\right],\end{displaymath}](img82.gif)