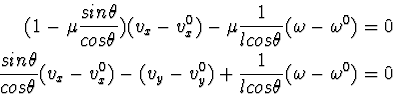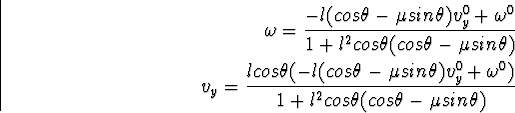Consider the rod sliding on a rough surface in Fig. 7. In
case of Coulomb friction, the friction force Ff depends
on the normal force FN by a constant coefficient ![]() , i.e.,
, i.e.,
![]() [6],
active in the direction opposite to vA,x, the velocity of the
contact point at the surface. Fy is the kinetic force
exerted by the center of mass in the vertical direction.
Combined with the gravitational force, Fg, this yields
the normal force FN = Fy + Fg
[6],
active in the direction opposite to vA,x, the velocity of the
contact point at the surface. Fy is the kinetic force
exerted by the center of mass in the vertical direction.
Combined with the gravitational force, Fg, this yields
the normal force FN = Fy + Fg
Let the variables be defined as in Fig. 7, and vx be the
horizontal velocity of the center of mass, M, vy the vertical
velocity, and ![]() the angular velocity. Fig. 7
shows that the linear velocities relate to the angular velocity as
the angular velocity. Fig. 7
shows that the linear velocities relate to the angular velocity as

In case of sliding motion, point A is in contact with the floor,
so vA,y = 0, which requires ![]() .This poses an algebraic constraint on vy and
.This poses an algebraic constraint on vy and ![]() , which
may cause impulses governed by conservation principles between the
two when initially this constraint is not satisfied.
As a result the friction force that is related to
, which
may cause impulses governed by conservation principles between the
two when initially this constraint is not satisfied.
As a result the friction force that is related to ![]() by
by
![]() may be of an impulsive nature. This impulse propagates into
may be of an impulsive nature. This impulse propagates into
![]() because of the
because of the
![]() constraint, and,
therefore, causes exogeneous
impulsive forces to interact with impulses due to conserved
quantities, and these forces are modulated by the change of value
of these quantities.
Refer to [7] for a detailed analysis.
constraint, and,
therefore, causes exogeneous
impulsive forces to interact with impulses due to conserved
quantities, and these forces are modulated by the change of value
of these quantities.
Refer to [7] for a detailed analysis.
According to the previous discussion,
the system equations can be compiled as
![\begin{displaymath}
{\small
\left.\begin{array}
{c}
\left[\begin{array}
{cccccc}...
... \\ 0 \\ 0 \\ -{F}_g \\ 0\end{array}\right]\end{array}\right.
}\end{displaymath}](img92.gif)
In this system of equations,
![\begin{displaymath}
\dot{\bar{x}} =
\left[\begin{array}
{c}
\dot{v}_{y} \\ \dot{...
...r{x} =
\left[\begin{array}
{c}
v_y \\ \omega\end{array}\right]\end{displaymath}](img93.gif)
![]()
The remaining equations in h yield
![\begin{displaymath}
\hat{y} =
\left[\begin{array}
{c}
F_y \\ F_f \\ F_N\end{array}\right]\end{displaymath}](img95.gif)
![\begin{displaymath}
F' =
\left[\begin{array}
{ccc}
0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 ...
...ay}
{ccc}
1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]\end{displaymath}](img96.gif)
and
![\begin{displaymath}
\hat{H}' =
\left[\begin{array}
{ccc}
0 & 1 & -\mu \\ -1 & 0...
...& 0 & 0 \\ 0 & 0 & 0 \\ 0 & -1 & -l cos\theta\end{array}\right]\end{displaymath}](img97.gif)
The pseude-inverse of F' is
![\begin{displaymath}
F'^+ =
\left[\begin{array}
{ccc}
0 & 1 & 0 \\ 1 & 0 & 0 \\ ...
...eta}{l cos\theta} & 0 & \frac{1}{l cos\theta}\end{array}\right]\end{displaymath}](img98.gif)
Therefore,
![\begin{displaymath}
\hat{H} F'^+ F'' =
\left[\begin{array}
{ccc}
1 - \mu \frac{...
...ta} & -1 & \frac{1}{l cos\theta} \\ 0 & 0 & 0\end{array}\right]\end{displaymath}](img99.gif)
results in