When a discrepancy between measurement and nominal value is detected,
a backward propagation
algorithm operates on the temporal causal graph to implicate component
parameters.
Implicated component parameters are labeled - (below normal)
and + (above normal). The algorithm propagates deviant
values backward on the directed edges
and consistent 
deviation labels are assigned sequentially
to vertices along the path if they do not have a previously
assigned value.
An example is shown in Fig. 10 for a deviant right tank
pressure, 
in the bi-tank system (Fig. 4).
initiates backward propagation
along 
and implicates 
below normal ( 
) or 
above normal ( 
). The next step along
implicates 
, and
implicates 
, and so on.
The algorithm operates depth-first, processing all instantaneous
edges before propagating along first-order changes, and so
on [10]. Propagation is
terminated along a path when a conflicting
assignment is reached. All component parameters along this
path are possible faults. As discussed in [10, 15],
observed normal
measurements do not terminate the backward propagation process
because the signal may be deviating in
reality. Due to error thresholds, it may just not be observed yet.
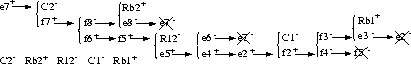
Figure 10: Backward propagation to find faults.