In a fast-breeder reactor,
heat from the reactor core is transported to
the turbine by a primary and secondary cooling system.
Liquid sodium is pumped through an
intermediate heat exchanger to transport heat from the primary cooling
loop to the feed water loop by means of a superheater and
evaporator vessel (Fig. 15).
Pump losses are modeled by 
.
The coil in the intermediate heat exchanger that accounts for
flow momentum build-up is represented by a fluid
inertia, 
.
The two sodium vessels are capacitances,
and 
.
An overflow column, 
, maintains
a desired sodium level in the main motor.
All connecting pipes are modeled as resistances.
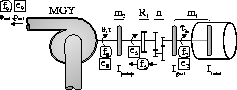
Figure 16: Synchronous ac motor that drives a pump.
The derivation of the causal relations of the sodium pump (Fig. 16)
are based on a
modulation factor g between input angular velocity, 
, and
output flow rate, 
, 
. Details are presented
in [10].
This factor is directly
proportional to and inversely proportional to ,
. The dependency of g on and 
can
be explicitly modeled by edges between these variables and the
affected variables. In case of the dynamic behavior, the affected variables
are input torque, 
, and output pressure, 
,
and the corresponding edges
are added to the causal graph (Fig. 17).
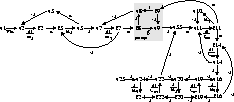
Figure 17: Temporal causal graph of dynamic behavior.
The dependency on system variables of the modulation factor
results in nonlinear, quadratic, behavior
, and, therefore, the relation on the
edge between and is unknown.
A sensitivity analysis of this
relation is shown in Fig. 18 and reveals that depending
on the values of and , the sensitivity of to
is positive or negative. Given the nominal values of the steady
state operation of the system, which is parameter dependent,
the weight of 
can be determined as a direct
(1) or inverse (-1) influence. However, once a deviation
occurs, and may differ from their nominal values
and a different operating point may be reached. Since these
new values are caused by failure, and, therefore, unknown,
the influence may reverse and is unknown as well.
Because this can only occur if
is predicted to be high based on the proportional influence (-1 or 1),
only a predicted decrease in is unambiguous, and, therefore,
propagated. A predicted increase in is propagated as
unknown.
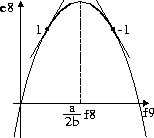
Figure 18: Detailed sensitivity analysis of
.
An overflow mechanism in the evaporator vessel maintains a maximum
level of liquid sodium (Fig. 15).
At this level, the excess liquid
sodium is drained by the overflow into the sump.
This exemplifies the configuration changes that may occur when
fault situations arise. During normal operation, there is a small
flow of liquid sodium through the overflow and the evaporator acts
as a source of constant pressure. However, when fault
situations arise, such as a blockage of the evaporator inlet, the
level may fall below the overflow and the evaporator changes its
behavior into that of a tank with given capacity. In the temporal
causal graph, this is incorporated by setting the level of liquid
in the evaporator, 
in Fig. 17, to unknown
whenever it is hypothesized to be high.