


Next: 3 Bond Graphs for
Up: 2 Background
Previous: 2.2 Nominal Values
Instead of just providing nominal values, the state estimation scheme
can be used for diagnosis by reconstructing the entire set of states
of the process if the process parameters have been
estimated precisely.
The reconstructed results are then compared and the set of
most consistent states is chosen as the best estimate.
This set can then be used to generate residuals based
on the actual observations to detect whether a fault
occurred.
To identify faults, the set of system equations are modified so that
the three basic types of faults listed below can be explicitly
identified as parameters and terms of the equations:
- Instrument faults; which refers to sensor faults.
- Actuator faults.
- Component faults; which refers to the different parts or
sub-systems in
the process where the fault can occur.
By explicitly incorporating these faults into the parameters of
system equations as part of the observer system, diagnosis algorithms
can be designed to detect and isolate faults.
A unifying
representation, in discrete form, is given by
(1) 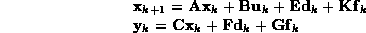
where 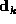 represents a disturbance term
due to noise, and
represents a disturbance term
due to noise, and 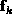 represents the effects introduced by the
fault term. Entries
of
represents the effects introduced by the
fault term. Entries
of 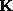 can be used to model actuator and component faults
and entries of
can be used to model actuator and component faults
and entries of 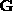 can be used to model sensor faults [6].
can be used to model sensor faults [6].
State estimation requires parameter estimation to determine precise
models of the process under scrutiny. Like state estimation schemes,
diagnosis schemes can be based on parameter
estimation techniques. The advantage of these schemes
is the close relation between estimated values and physical coefficients.
Given that nominal values can be derived from state
estimation schemes or from design documents, comprehensive
diagnosis can proceed by performing one or
several of the following techniques (Fig. 3):
- Quantitative parameter estimation is derived from
numerical models of the process. Typically
filtering methods may be applied
to estimate system parameters based on a vector of
residuals. These parameters represent aggregate behavior of
process components, and, therefore, a fault may cause a number of
parameter deviations.
This process
is computationally intensive, and may be subject to the convergence
problems that occur in numerical estimation. To improve
performance,
other techniques can be used to narrow down the
parameter search space.
- Performance of diagnosis algorithms can be enhanced
by incorporating sophisticated
sensitivity analysis schemes. The degree to which different
faults affect measurements can be
exploited by the parameter estimation procedure to rank possible
causes by the sensitivity of the observables to the hypothesized causes.
- Failure mode mappings
can further enhance the fault identification and isolation process.
They represent a discrete event systems approach that
requires knowledge about how
process components may fail, and what effects these failures have
on system parameters.
- Dependency analysis techniques
rely on a topological
functional model of the process and capture a weighted dependency
between parameters and measured variables. These weights could be
a function of various parameters, such as proximity to the observed
fault. Sometimes the weights may
capture process delay times, and in such cases the
dependency graph represents a dynamic model of system behavior.
Observed deviations can be traced back to parameter values which can
be ordered in terms of when their effects become active.
Note that the techniques described above are not mutually exclusive.
Any of these methods can be effectively developed into a diagnosis
system. However, developing a diagnosis framework that integrates
two or more of these approaches is likely to produce more efficient
and robust systems. It remains a challenge to see how best to
develop such systems.
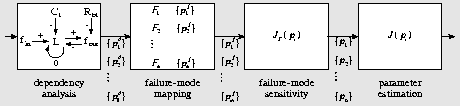
Figure 3: Complementary diagnosis schemes.



Next: 3 Bond Graphs for
Up: 2 Background
Previous: 2.2 Nominal Values
Pieter J. Mosterman
Tue Jul 15 11:26:35 CDT 1997
![]()
![]() represents a disturbance term
due to noise, and
represents a disturbance term
due to noise, and ![]() represents the effects introduced by the
fault term. Entries
of
represents the effects introduced by the
fault term. Entries
of ![]() can be used to model actuator and component faults
and entries of
can be used to model actuator and component faults
and entries of ![]() can be used to model sensor faults [6].
can be used to model sensor faults [6].
