When a system operates in the sliding regime, the dynamics of the system along the sliding surface is not defined in a continuous sense. We adopt the notion of equivalence dynamics for the sliding regime justified by Filippov [3, 9]. Consider the switching surface as an infinitesimal band rather than a crisp border. The equivalence dynamics on the surface is defined as the limiting behaviors when the width of the band tends to zero. This construction preserves the physical meaning of the dynamics at the discontinuous boundaries. Furthermore, it serves as a basis for algorithmically determining the direction and magnitude of the sliding motion.
Assume 
is the thickness of the hysteresis band around the
sliding surface (see Fig. 17). If is small, the
fields 
and 
on either side of the surface can be
represented by their instantaneous vector representations with normal
components 
and 
, and tangential components
and 
. The direction of movement is along the
sliding surface, and we need to calculate the average velocity on the
surface.
We compute the time the system takes to cross the band as
and
,
and the tangential distance the system has travelled over two adjacent
time intervals ( 
) as:
(5) 
Then we compute the average velocity of the motion on the surface:
(6) 
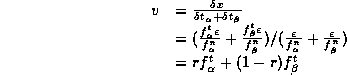
where 
.
Thus, the vector v is on the line connecting the end points of
and ,
with r and 1-r as its barycentric coordinates (Fig. 18).
Let c be the difference vector 
,
and p be the intersection
of c with the tangent vector. Let p partition c into two segments, d
and e.
We have 
by triangle congruence.
Thus, we have shown that the barycentric coordinate for p is the same
as that for v (recall 
).
This corresponds to Filippov's construction, i.e., the
vector v is the same as the tangent vector.
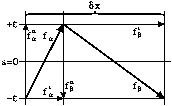
Figure 17: Motion along a sliding surface.
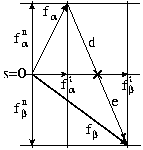
Figure 18: Filippov construction of sliding motion direction and magnitude.
In fact, the formula 
can be used to compute v, where r is determined from the normal
components of the two vector fields if the angle between the sliding
surface and vector fields is known.