As illustrated by the bouncing ball, mode switching may involve
jumps in the phase space. Consider
collision effects that may occur in a cam-follower system in automobiles
(Fig. 13). The cam mechanism is used to translate rotational
motion into a linear displacement to open and close valves in the
engine cylinders. Typically, a spring mechanism is used to ensure
contact between the rod and rotating cam but due to the high
velocities of operation (up till several thousands of
revolutions per minute) and wear of the spring, the rod may bounce
on and off the cam, causing collisions.
These collisions can be modeled by Newton's
law using a coefficient of restitution, 
, to
model loss of energy during collision
.
Typically, is a function of impact velocities [2],
and a threshold, 
, can be set below which the collision
is considered perfectly non-elastic (i.e., 
).
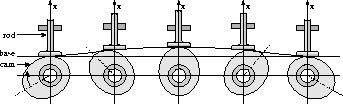
Figure 13: A cam mechanism opens a valve.
To analyze the phase space of the cam-follower, consider the valve and rod mechanism moving with only the valve spring and rocker arm friction acting.
(3) 
The phase space is shown on the left in Fig. 14. The valve spring and combined inertias result in a second order system with friction. Therefore, the rod velocity oscillates between positive and negative with a decreasing amplitude. When the cam mechanism is included, the rod velocity follows an ellipsoid path as shown in the right phase space diagram in Fig. 14.
(4) 
If the rod and cam positions are equal and the rod velocity is more negative than the cam velocity, collision occurs like the bouncing ball in Fig. 4, and in case the collision is perfectly non-elastic, the rod velocity instantaneously equals the cam velocity. This is indicated by the grayed out areas of the phase space. The rod disconnects from the cam if its deceleration is larger, which corresponds to the steeper curve in the left half-plane. This is shown in Fig. 15 for one simulation run.
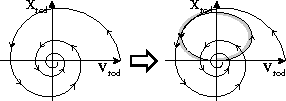
Figure 14: Phase space of the cam-follower.
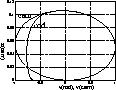
Figure 15: The rod may disconnect, 
.
Numerical approximations of the rod parameters may cause the simulation
to show the rod disconnects
at one time and ends up in the grayed out area of the phase space
shown in Fig. 16 where collision occurs and the rod
takes on the same velocity as the cam. Now, the rod and cam are
connected again, but the next simulation step may result in them
disconnecting and chattering occurs along the switching surface
and 
as shown on the right in Fig. 16.
Like the evaporator, chattering is an artifact of the
simulation caused by
model abstraction. In reality, higher order effects
like the rod's elasticity and
adhesive forces between the rod and cam surfaces
ensure it is connected for a short while before disconnecting.
When the values of these parameters tend to 0, the system
behavior starts to
slide along the surface.
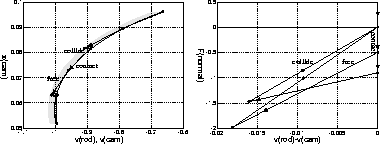
Figure 16: Numerical simulation may result in chattering, C=0.01.