To model hybrid dynamic systems, the mathematical model has to be
implemented by a model that supports the idiosyncrasies of dynamic
physical systems.
In physical system models, event generation 
is based on
continuous signals and separated from the discrete model part, 
,
[6].
Furthermore, event generation often is specified in terms
of signal values, s, that are
derived from state variables given a mode 
, 
.
Fig. 7 shows the implementation model.
In this model mythical modes emerge from two loops
which results in mythical modes without discontinuous changes
in the state vector. Therefore, it allows sequences of mythical modes on
transitions.
which
results in mythical
modes when discontinuous changes in the state vector occur. Given
temporal evolution of state, this can only occur on 
transitions.
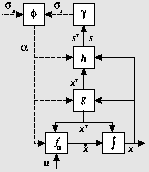
Figure 7: A general hybrid system.
The recursive relation in Eq. (6) is implemented
by SEL_MODE which
is presented in Algorithm 1.
SEL_MODE is executed twice for each time step.
First when a new mode based on continuous evolution is determined.
To improve precision, 
is variable and a bisectional search
is used to find the switching point within a pre-specified accuracy.
Second when pinnacles are traversed, and,
therefore, the argument of SEL_MODE
in Algorithm 1 is set to 0.
The DER_SIGNAL function deals with numerical effects of
the derivative part of h, 
, as a special case.
In case either 
(a pinnacle),
or if 
(a discontinuous change),
the area of the corresponding Dirac
pulse is returned without including the signals that do not contain
derivative effects
as embodied by 
. Otherwise, no discontinuous changes occur
and an Euler approximation can be used for the derivative, in which case
signals as a result of are included.
