A causal structure can be imposed on a bond graph model, using
local constraint relations among the components associated with a
junction.
A systematic algorithm for causality assignment is the
Sequential Causality Assignment Procedure
(SCAP) [21]. This algorithm categorizes
local constraints as (1) enforced causality, by
sources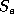 
and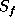 
, (2) preferred causality,
for energy storage elements, C and I, and (3) indifferent
causality for resistances R. The constraints are applied in
the order above, with an effort source always imposing an effort
(e.g., pressure)
causality on a junction and a flow source always imposing a flow
(e.g., volume flow)
causality on a junction. Opposite assignment of causality
to a source indicates a physical incorrectness of the model, e.g.,
a shorted voltage source. The preferred causality for energy storage elements
is for them to operate as integrators as opposed to differentiators.
The integral relation establishes natural dependence among the effort or
flow variables associated with a bond.
For example, the implication of the integral form for
a C element is that it prefers to deliver effort on a
junction, i.e.,
(2) 
An I element prefers to enforce flow on a junction, i.e.,
(3) 
Resistive elements have no preference of causality, they conform with how they are driven.
Consider the bi-tank system and its bond graph
in Fig. 4. Fig. 5 depicts the causality assignment
procedure.
The first step selects the
flow source, 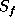and assigns it flow causality which means
it enforces flow on the adjacent 0-junction. By convention, the
direction of effort is shown by a perpendicular stroke at one end
of a power bond. Since flow is enforced on the 0-junction,
effort is enforced on the flow source,
depicted by the perpendicular stroke at the
beginning of its connecting bond (1) in Fig. 5.
Because the flow constraint on a 0-junction requires the sum of all
flows to equal zero, the flow values of the two remaining bonds are
still undetermined. Therefore, the assigned causality does not
propagate any further.
In the second step, the capacity 
is selected
and enforces effort on its adjacent
0-junction depicted by the perpendicular stroke at the end
of bond (2).
Because a 0-junction represents an equal pressure junction,
this enforced pressure propagates across all other connected
bonds, (3) and (4).
So,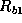 
determines the outflow of given this pressure.
Again, the effort causality on the connecting 1-junction does
not propagate any further.
In the third step,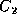 
is selected and its
preferred causality enforces effort on the 0-junction
through bond (7) which propagates across the other
connected bonds (6) and (8).
This results in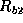 
determining the outflow
of 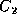, bond (8). By default the
remaining bond of the connecting 1-junction (common flow)
(5) has to impose effort causality
on the connecting resistance,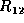 
, which determines the flow
between and .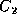
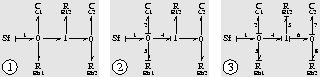
Figure 5: Algorithmic assignment of causality.