The dynamic aspects of bond graph models establish temporal relations between deviant observations and hypothesized abrupt parameter changes, or faults.
Faults affect certain parts of the system instantaneously, whereas their effect requires time to propagate to other parts. So, relations can be instantaneous or delayed. Delays can be further classified by the order of the effect, e.g., a first order or a second order delay.
Determining the new state vector after an abrupt fault is key to analyzing
parameter deviation effects for the fault isolation task.
Abrupt changes in the parameter values of energy
storage elements may require an abrupt change of the state vector based on
the principle of conservation of state [10, 16].
To illustrate, assume that at time 
, a
rock falls into an open tank with capacity
C, which has an outflow resistance R for a connected outlet
pipe (Fig. 6).
The capacity of the tank decreases abruptly to C', and,
therefore, the pressure, p, at the bottom changes instantaneously
to 
, because
and the amount of liquid in the tank, q, is conserved.
The possible effects of
changes in the tank capacity, C, and outflow resistance,
R, on the state variables
p and q with their behavior equations are shown in Fig. 6.
In faulty
situations one has to take into account the time-varying effect
of the component parameters in the system. In this situation, for capacity
C the constituent equation becomes
.
Therefore, 
.
An abrupt change in C results in an instantaneous jump in
, implying an immediate abrupt
change in p. Thus the discontinuous change
in the system state as a result of an abrupt parameter change is
made explicit. In the integral form of constituent equations,
, used in bond graphs,
this effect is automatically incorporated, since
.
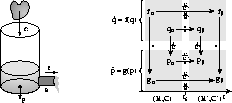
Figure 6: Transfer of the state vector and its field across discontinuous
change.
To extend bond graph modeling to component oriented diagnosis requires establishing correspondence between individual components and bond graph elements. In the bond graph framework, primitive elements, such as resistors and capacitors represent mechanisms which may not always be in one-to-one correspondences with individual system components [3]. An individual component may have multiple aspects represented in the bond graph. For example, a component such as a pipe may be represented in the bond graph by its build-up of flow momentum (I) and resistance to flow (R). Biswas and Yu [3] describe a compositional methodology for deriving bond graph models for diagnosis from a physical system description so that the bond graph elements directly correspond to system components and mechanisms under diagnostic scrutiny. The modeling methodology has been further instantiated by Mosterman and Biswas [12, 13, 16].