For the bouncing ball, all CSPEC transitions are specified
in terms of switching invariant state variables (Fig. 8), except
for the force ![]() which is
which is
![]() where g is the gravitational force.
To derive the conditions under which the
flow source, i.e., junction
where g is the gravitational force.
To derive the conditions under which the
flow source, i.e., junction ![]() turns off,
turns off,
![]() has to be expressed in terms of stored energy variables
has to be expressed in terms of stored energy variables
![]() and
and ![]() . When the flow source is
active, buffer dependency causes
. When the flow source is
active, buffer dependency causes ![]() to be derivative, i.e.,
to be derivative, i.e.,
and, discontinuous changes induce a Dirac pulse, ![]() . From the
CSPEC for
. From the
CSPEC for ![]() , the condition for switching is
, the condition for switching is
![]() .
When this junction is in its off state,
.
When this junction is in its off state, ![]() .
When it switches on, the velocity and momentum of the ball become
0 instantaneously. From equation (1), this implies that
.
When it switches on, the velocity and momentum of the ball become
0 instantaneously. From equation (1), this implies that
![]() becomes a Dirac pulse whose magnitude approaches positive or
negative infinity, depending on whether
the stored momentum was negative or positive, respectively. If the
momentum was 0,
becomes a Dirac pulse whose magnitude approaches positive or
negative infinity, depending on whether
the stored momentum was negative or positive, respectively. If the
momentum was 0, ![]() equals 0. Let the function sign be
defined as
equals 0. Let the function sign be
defined as
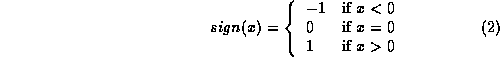
If ![]() the condition for switching becomes
the condition for switching becomes ![]() .
Because of the magnitude of the Dirac pulse, the effects of friction and
the gravitational force can be neglected at switching.
Therefore, the condition for the on-off state transition for
.
Because of the magnitude of the Dirac pulse, the effects of friction and
the gravitational force can be neglected at switching.
Therefore, the condition for the on-off state transition for
![]() is
is ![]() This inequality holds for all values of p ;SPMgt; 0. If p=0 then
This inequality holds for all values of p ;SPMgt; 0. If p=0 then ![]() and
and ![]() . The condition becomes
. The condition becomes ![]() which is never
true for g=-9.81.
The area for which transition occurs is represented by p;SPMgt;0 which
is grayed out in the phase space, shown in Fig. 9.
which is never
true for g=-9.81.
The area for which transition occurs is represented by p;SPMgt;0 which
is grayed out in the phase space, shown in Fig. 9.
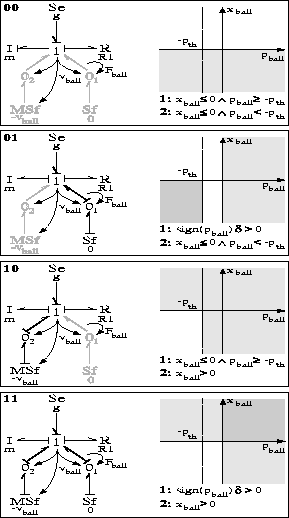
Figure 9: Energy phase space: Bouncing Ball.
Phase spaces are established (Fig. 9) for each of the four modes of the combined elastic and non-elastic collision and labeled 00, 01, 10, and 11, where the first digit indicates whether the controlled junction 2 is on (1) or off (0), and the second digit indicates the same for controlled junction 1. In the phase spaces the areas that are instantaneously departed are grayed out and the conjunction of the four energy phase spaces is shown in Fig. 10. This phase space shows that there is an energy distribution which does not correspond to a real mode of operation. Since the dimensions of the energy phase space are invariant across switches, this energy distribution cannot reach a real mode of operation during a sequence of switches, thus violating the divergence of time condition.
In this area, when the ball hits the floor, it has positive momentum. For the bouncing ball, this mode is unreachable, and, therefore, the model is physically consistent: The system always moves towards a negative momentum and it instantaneously reverses (depicted by double arrows in Fig. 10) when the displacement becomes zero. Analytically the displacement never becomes negative. However, due to numerical disturbances, or initial conditions, the model may arrive in the physically inconsistent area of operation, especially, in case the floor is another moving body. Therefore, in such situations, when simulating the system, the CSPEC conditions model the desired physical scenario inadequately.
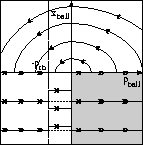
Figure 10: Conjunction of the multiple energy phase spaces.
To establish a physically correct system, the CSPEC switching
conditions have to be modified. From the physical system it is
clear that additional constraints can be imposed based on the
momentum of the ball. Since the switching conditions of the
controlled junction 1 are not mutually exclusive, the conditions
![]() and
and ![]() can be added to
the off/on and on/off transitions, respectively. This results
in the
energy phase spaces shown in Fig. 11. Now, the
conjunction of the energy phase spaces results in
a real mode of operation for each energy
distribution. Because of the combinatorial switching logic, this
real mode of operation is reachable in one switching step. A
simulation of the physically consistent system is shown in
Fig. 12. The air resistance (R1), causes the bounce
of the ball to dampen until the momentum of the ball falls below
the threshold value
can be added to
the off/on and on/off transitions, respectively. This results
in the
energy phase spaces shown in Fig. 11. Now, the
conjunction of the energy phase spaces results in
a real mode of operation for each energy
distribution. Because of the combinatorial switching logic, this
real mode of operation is reachable in one switching step. A
simulation of the physically consistent system is shown in
Fig. 12. The air resistance (R1), causes the bounce
of the ball to dampen until the momentum of the ball falls below
the threshold value ![]() and the ball comes to rest on
the floor.
and the ball comes to rest on
the floor.
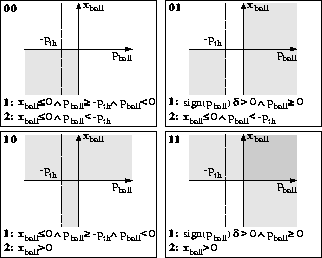
Figure 11: Modified multiple energy phase spaces.
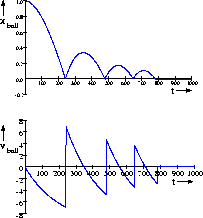
Figure 12: Bouncing ball: Physically consistent simulation.