When two or more buffers become dependent, redistribution of
the state variable values according to the buffer ratios is required.
For the energy phase space analysis this means that a number of
dimensions collapse into one. This is illustrated by the
two capacitor system in Fig. 13. When the relay is open,
the capacitors are independent and charge individually. When
the voltage difference between the two crosses a threshold value,
say 0, the relay closes and the capacitors become dependent,
causing an immediate redistribution in charge (state variable) among
the capacitors so both capacitors have the same effort value,
.
Substitution of these values for 
and 
in the relay's
CSPEC yields the switching condition
.
This is true in the entire energy phase space (Fig. 14).
Notice that a degree of freedom is lost because the buffer dependency
causes the two-dimensional phase
space to collapse into a one-dimensional phase space. When
the two energy phase spaces are analyzed, it is apparent that
divergence of time is not guaranteed. The inconsistency results
from the equal sign in the switching off condition for the relay.
When the relay is on, and both voltages become equal it will be
switched off instantaneously and vice versa.
To solve this problem,
the condition for switching needs to be changed to 
. Then the
relay does not switch out of its on state and divergence of time
is guaranteed. This example illustrates that the energy
phase space analysis applies even when dependency
relations among the buffers cause changes in the system model.
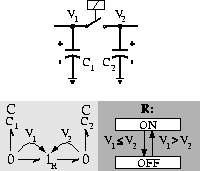
Figure 13: Dependent capacitors.
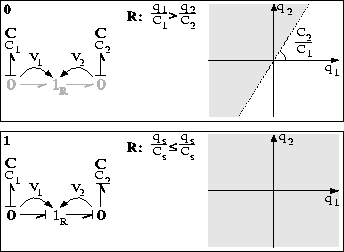
Figure 14: Dependent Capacitors: Energy phase spaces.