Having established the invariance of state principle, the next step is to establish systematic methods for verifying system models that incorporate discontinuous changes. Given the existence of instantaneous mode changes, it is important to establish that mythical transitions do not result in loops and violate the principle of divergence of time.
As a case of interacting discontinuous changes, consider the two ball examples of the last section. Assume that
),
an ideal elastic collision occurs,
The ball bounce is modeled to be ideally elastic, and the amplitude of
the bounce decreases with time because of air resistance. Thus its
momentum decreases with every bounce, and once it falls below a
certain threshold value, , the ball is observed to come to
rest.
This part of the behavior is modeled as an
ideal non-elastic collision. The hybrid model for this system is shown
in Fig. 8. The system model has two interacting switches, and
this raises the issue of divergence of time. To verify that the system
model satisfies this condition, a multiple energy phase space
analysis technique has been developed.
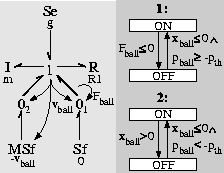
Figure 8: A combined ideal elastic and non-elastic collision.
Phase space analysis is based on a qualitative representation of model behavior. The energy phase space is k-dimensional, where k is the number of independent buffers or state variables in the system. These energy variables cannot change discontinuously across a sequence of mythical modes, therefore, mythical mode points in this space are invariant and correspond to continuous state vectors of the model. To establish phase space behavior of a hybrid model in terms of its energy distribution, its switching conditions have to be expressed in terms of stored energy (i.e., generalized momentum and generalized displacement). However, switching conditions in the model CSPECs are based on power variables which can be composed of different state variables, depending on the mode of operation. Therefore, an energy phase space has to be constructed for each mode of operation. The rest of this section studies the energy phase space for both the source-buffer and the buffer-buffer dependency conditions that may arise in system models.