


Next: 3.2 Evolution of System
Up: 3 Analyzing Model Discontinuities
Previous: 3 Analyzing Model Discontinuities
As a first step, we analyze discontinuous changes by considering
the bullet-wood non-elastic collision illustrated
in Fig. 1. Conservation of momentum
determines that after collision both masses have a common velocity,
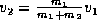 . The
amount of energy contained in the system before the collision is
. The
amount of energy contained in the system before the collision is
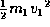 , and, the amount of energy in the
system after the collision
is
, and, the amount of energy in the
system after the collision
is 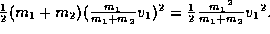 This implies that the collision causes a loss of energy equal to
This implies that the collision causes a loss of energy equal to
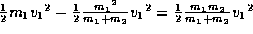 .
Imposition of conservation of momentum results in a
discontinuous loss of energy to the environment, and is represented
by a Dirac pulse
.
Imposition of conservation of momentum results in a
discontinuous loss of energy to the environment, and is represented
by a Dirac pulse whose area is determined by the model.
The explanation for this energy loss is that an instantaneous change in
system configuration results in two independent buffers (the masses)
becoming dependent, which then causes dissipation of energy to the
environment as heat.
In case the environment is considered isothermal, this thermal
energy flow need not be explicitly modeled
by a heat sink between the system and the environment
(like dissipation of resistive elements).
Note that the instantaneous loss of energy would not occur if a resistive
element modeled material deformation between the buffers
(i.e., their connection was non-ideal).
whose area is determined by the model.
The explanation for this energy loss is that an instantaneous change in
system configuration results in two independent buffers (the masses)
becoming dependent, which then causes dissipation of energy to the
environment as heat.
In case the environment is considered isothermal, this thermal
energy flow need not be explicitly modeled
by a heat sink between the system and the environment
(like dissipation of resistive elements).
Note that the instantaneous loss of energy would not occur if a resistive
element modeled material deformation between the buffers
(i.e., their connection was non-ideal).
From a physical perspective, buffers that become dependent have to be
analyzed carefully. Bond graph modeling theory assumes
that physical system behaviors change slowly enough
to satisfy the lumped parameter assumption
where distribution of energy
within energy buffers is considered homogeneous. Therefore, phenomena like
dynamic turbulence effects caused by sudden large pressure differences
in a tank cannot be easily taken into account in system models. The
observation of an instantaneous energy redistribution when buffers
become dependent is basically an artifact of an abstract model operating
on a coarse time scale.
To study the lumped parameter assumption in detail,
consider the free expansion
experiment conducted by Gay-Lussac and Joule shown in Fig. 4
[3]. A chamber is made up of two connected bulbs with an
on-off valve that switches the connection on or off. Initially, only the
left bulb contains a gas and the valve is closed. When the valve
connecting the two volumes is opened, the gas in the left bulb
expands freely and starts diffusing into the right bulb. Even if the
connecting orifice is non-resistive this diffusion introduces
turbulence effects that result in non-homogeneities,
which violate the lumped parameter assumption. From a thermodynamics
perspective, when the goal is to compute equilibrium temperatures
and pressures, using energy balance on a homogeneous model is
adequate.
For the dynamic effects to be
negligible in the time scale of interest, they have to occur in
a mode of continuous operation.
In case of the above experiment, if the valve were
closed quickly enough after opening, i.e., we have two
instantaneous changes, the gas cannot diffuse
and the homogeneous distribution over both of the volumes
is never actually established. For CSPEC conditions based on the energy
variables involved, the
time scale is too small for the lumped parameter assumption to hold,
and bond graphs cannot be used to model such processes.
In effect, an immediate closing of the opening leads to no redistribution
of energy which substantiates the observation that
there never was a connection in real time.
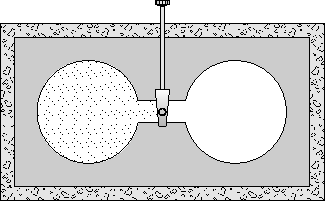
Figure 4: Instantaneous free expansion of a gas by diffusion.
In conclusion, switching conditions based on energy stored
in buffers that are between dependent and independent
without an intervening mode of continuous operation are inconsistent
with bond graph assumptions and, therefore, prohibited.
In this case, either model refinement
or another modeling approach has to be chosen.



Next: 3.2 Evolution of System
Up: 3 Analyzing Model Discontinuities
Previous: 3 Analyzing Model Discontinuities
Pieter J. Mosterman
Mon Jul 21 19:58:19 CDT 1997
 whose area is determined by the model.
The explanation for this energy loss is that an instantaneous change in
system configuration results in two independent buffers (the masses)
becoming dependent, which then causes dissipation of energy to the
environment as heat.
In case the environment is considered isothermal, this thermal
energy flow need not be explicitly modeled
by a heat sink between the system and the environment
(like dissipation of resistive elements).
Note that the instantaneous loss of energy would not occur if a resistive
element modeled material deformation between the buffers
(i.e., their connection was non-ideal).
whose area is determined by the model.
The explanation for this energy loss is that an instantaneous change in
system configuration results in two independent buffers (the masses)
becoming dependent, which then causes dissipation of energy to the
environment as heat.
In case the environment is considered isothermal, this thermal
energy flow need not be explicitly modeled
by a heat sink between the system and the environment
(like dissipation of resistive elements).
Note that the instantaneous loss of energy would not occur if a resistive
element modeled material deformation between the buffers
(i.e., their connection was non-ideal).
