A consequence of the absence of a physical manifestation of mythical modes is that the system cannot exchange energy with its environment during a sequence of discontinuous changes, in other words, it is isolated. This is compatible with the fact that there is no redistribution of stored energy within the system during such a sequence.
The principle that energy is not redistributed during discontinuous, instantaneous changes, but only after a new mode is reached is termed the principle of invariance of state. The mythical mode algorithm for deriving discontinuous changes, and the corresponding model verification technique are based on this principle.
Consider an ideal elastic collision, Fig. 5.
When the ball hits the floor with a velocity v, it induces a force
which results in a reaction force by the floor. In case of an
ideal elastic collision this causes the
ball to instantaneously reverse its velocity and start traveling upwards.
In the corresponding hybrid bond graph model, the change of velocity
is shown as a modulated flow source
which delivers its power when the controlled junction 
comes on.
The CSPEC specifies that this occurs at the point when the
ball hits the floor. The moment the ball starts
to move upwards, the controlled
junction turns off and the ball is represented by a separate model
fragment again. The floor is represented as a source to indicate it
is part of the system environment and the amount of energy transferred
back to the ball from the floor becomes a modeling decision.
The change in momentum of the ball can only occur when a real mode
is reached after mythical transitions.
In general, any transfer of energy into or
out of the system can only be applied in the real mode. However, during
mythical transitions, a Dirac pulse may be generated and cause further CSPEC
transitions. Once generated, their effect on all
CSPECs have to be analyzed immediately. If
the Dirac pulses can be propagated without causing another CSPEC
transition, the current mode is established as a real one and the effect
of the Dirac pulse is taken into account when computing the new state
vector in this mode.
Otherwise, this mode is labeled as mythical, and the active
CSPEC is used to generate the next mode, and the analysis continues as
before without actually propagating the Dirac pulses.
Thus invariance of state holds
across a series of mythical mode changes and the continuous state
vector is invariant to mythical switches.
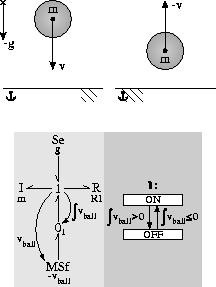
Figure 5: Ideal elastic collision.
To correctly infer model configuration changes, all buffers that become dependent have to be analyzed in derivative causality, i.e., they generate Dirac pulses. Changes in configuration and independence of buffers may lead to further model switches.