After mythical changes, when a new continuous mode of system operation is established, the initial state vector in the new mode has to be derived from the last system state in the previous continuous mode. The energy stored in buffers that remain independent does not change in the new configuration because of the integral relation they impose on their energy variables. However, the energy content of dependent buffers can change as determined by the conservation of state principle[3, 13] which states that state variable (charge and momentum) values are conserved. The dependence causes redistribution of the total energy in the buffers, in the ratio of their parameter values as demonstrated by the bullet-wood system.
In case buffers become dependent upon sources,
their energy changes according to the signal enforced by
the source. An ideal non-elastic collision, depicted in
Fig. 6, shows the discontinuous change causing a
source-buffer dependency with no dissipative effects (ideal
collision). In the hybrid bond graph model this is depicted as a flow
source of 0 value that gets switched in at the time of collision.
Notice that the momentum in the system before collision,
![]() , becomes 0 instantaneously. Conservation
of state cannot be applied to derive the new value of the stored
energy in the dependent buffer. Instead, this value is completely
determined by the value of the connected source.
, becomes 0 instantaneously. Conservation
of state cannot be applied to derive the new value of the stored
energy in the dependent buffer. Instead, this value is completely
determined by the value of the connected source.
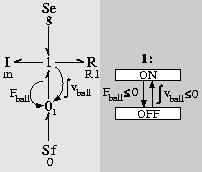
Figure 6: Ideal non-elastic collision.
In actuality, the ball and floor could be modeled as one system. For the elastic collision, the floor is modeled as a buffer with a large stiffness coefficient, producing the behavior shown in Fig. 7 (x is the displacement, and v the velocity of the object). For the non-elastic collision, the floor is modeled as a large resistance, which dissipates energy, and this brings the ball to a halt with a very fast time constant. For these models, source-buffer dependencies and modeled Dirac sources do not occur, and conservation of state and energy is not violated. Therefore, the apparent violation of these principles can be directly attributed to buffer dependencies in the model.
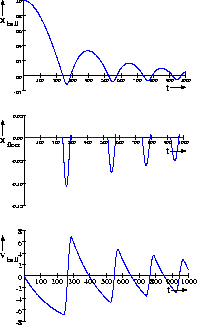
Figure 7: Ideal elastic collision with the floor modeled as having
a relatively large stiffness.
The above examples illustrate that three situations can be associated with the initial value problem that results from discontinuities in a model: