Consider the hydraulics of the evaporator vessel
in Fig. 1. There is
a constant inflow of liquid into the tank, ![]() , and an outflow,
, and an outflow,
![]() , that depends on the pressure in the tank
and the Bernoulli resistance,
, that depends on the pressure in the tank
and the Bernoulli resistance, ![]() .
The physical system has two distinct modes of operation; mode
.
The physical system has two distinct modes of operation; mode ![]() where the overflow is not active, and mode
where the overflow is not active, and mode ![]() where it is.
The overflow mechanism becomes active when the liquid level in the
evaporator, L, exceeds a threshold value,
where it is.
The overflow mechanism becomes active when the liquid level in the
evaporator, L, exceeds a threshold value, ![]() , which causes
a flow
, which causes
a flow ![]() through a narrow pipe with resistance,
through a narrow pipe with resistance, ![]() , and
inertia, I. When the overflow mechanism becomes active, the
pipe inertia starts to build up flow momentum, p,
until its flow maintains
a steady level, i.e.,
, and
inertia, I. When the overflow mechanism becomes active, the
pipe inertia starts to build up flow momentum, p,
until its flow maintains
a steady level, i.e., ![]() .
.
(1) ![]()
(2) ![]()
Suppose initially the system is in mode ![]() , the flow of liquid
through the narrow pipe is zero and the tank fills.
In steady state, the pressure causes an outflow through
, the flow of liquid
through the narrow pipe is zero and the tank fills.
In steady state, the pressure causes an outflow through ![]() that
equals the inflow,
that
equals the inflow, ![]() , of fluid in the tank.
If the level, L, becomes
higher than the threshold level,
, of fluid in the tank.
If the level, L, becomes
higher than the threshold level, ![]() ,
the system will move into mode
,
the system will move into mode ![]() as shown
in Fig. 8 against time (left) and in phase space (right).
Now there is another path of liquid flowing
out of the tank and it may continue to fill at a slower pace
and reach a steady state level,
as shown
in Fig. 8 against time (left) and in phase space (right).
Now there is another path of liquid flowing
out of the tank and it may continue to fill at a slower pace
and reach a steady state level, ![]() , which causes a total
outflow equal to its inflow. This new steady state liquid level
is below what would have been attained had the overflow
mechanism not been present.
, which causes a total
outflow equal to its inflow. This new steady state liquid level
is below what would have been attained had the overflow
mechanism not been present.
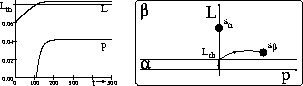
Figure 8: After an initial transient stage, the evaporator level
reaches steady state.
More complicated behavior is exhibited when ![]() is higher than the level
at steady state in mode
is higher than the level
at steady state in mode ![]() , Fig. 9.
When the moment the overflow becomes active,
the system moves towards a steady state with lower pressure which
causes the level to drop and the overflow mechanism turns off.
In the separate phase spaces for each mode,
, Fig. 9.
When the moment the overflow becomes active,
the system moves towards a steady state with lower pressure which
causes the level to drop and the overflow mechanism turns off.
In the separate phase spaces for each mode, ![]() and
and ![]() ,
the grayed out areas represent state vector values that
cause a transition to the other mode. The fields in
each mode are directed towards the switching border
represented by
,
the grayed out areas represent state vector values that
cause a transition to the other mode. The fields in
each mode are directed towards the switching border
represented by ![]() , and, therefore, independent of the
initial conditions. In time, the system reaches a point where it moves
from one mode to the other and back immediately and chattering
occurs (Fig. 10).
, and, therefore, independent of the
initial conditions. In time, the system reaches a point where it moves
from one mode to the other and back immediately and chattering
occurs (Fig. 10).
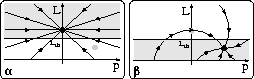
Figure 9: Phase space of behavior in each mode.
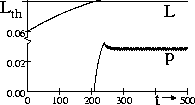
Figure 10: Chattering between modes with an active and inactive overflow,
![]() .
.
Analysis of system behavior for this configuration
requires a physically consistent treatment of state evolution at ![]() .
Since the domains of the fields for each mode are mutually
exclusive, the phase spaces can be combined into one. Fig. 11 depicts
three qualitative scenarios by which
.
Since the domains of the fields for each mode are mutually
exclusive, the phase spaces can be combined into one. Fig. 11 depicts
three qualitative scenarios by which ![]() may be approached.
In the scenario
marked 1, the system approaches
may be approached.
In the scenario
marked 1, the system approaches ![]() with a field component in the
-p direction in
with a field component in the
-p direction in ![]() which is the active mode of operation for
which is the active mode of operation for ![]() .
In scenario 2, the
system approaches
.
In scenario 2, the
system approaches ![]() with a 0 component in the p direction
in
with a 0 component in the p direction
in ![]() .
In scenario 3, the fields of
.
In scenario 3, the fields of ![]() and
and ![]() have equal
angles and opposite direction when approaching
have equal
angles and opposite direction when approaching ![]() from
from ![]() .
The objective is to
determine which one of these is at equilibrium when
.
The objective is to
determine which one of these is at equilibrium when ![]() is reached.
is reached.
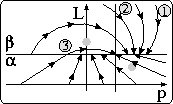
Figure 11: Concatenation of pieces of phase spaces from modes ![]() and
and ![]() .
.
To investigate physical behavior, we first observe that in reality the border
between the modes of operation is not as crisp as modeled. Modeling
abstractions disregard small parameters that
are present and affect behavior at the boundary, ![]() . For example,
though small, forces at the rim of the overflow pipe require the
fluid level in the tank to be somewhat higher than the rim in order for
liquid to start pouring in. During the time interval that this
excess level is drained, the overflow mechanism is active, and the
level continues to fall. So, after becoming active, in reality a period
of time elapses before it turns off again. Other higher order
physical phenomena, such as cohesive forces in the liquid, smooth
the discrete switching behavior and a small continuous flow of
liquid through the overflow is realized.
. For example,
though small, forces at the rim of the overflow pipe require the
fluid level in the tank to be somewhat higher than the rim in order for
liquid to start pouring in. During the time interval that this
excess level is drained, the overflow mechanism is active, and the
level continues to fall. So, after becoming active, in reality a period
of time elapses before it turns off again. Other higher order
physical phenomena, such as cohesive forces in the liquid, smooth
the discrete switching behavior and a small continuous flow of
liquid through the overflow is realized.
Other physical effects cause similar hysteresis at the boundary
between operational modes, and this can be used to derive correct model
semantics for behavior at this boundary. Fig. 12 shows
the effect of a ![]() hysteresis band around
hysteresis band around ![]() .
Clearly, the system converges to a recurring point on
.
Clearly, the system converges to a recurring point on ![]() and
and ![]() and starts to oscillate between them. If
and starts to oscillate between them. If
![]() is taken, these recurring points coincide
and the field resultant at the common point on
is taken, these recurring points coincide
and the field resultant at the common point on ![]() can be determined based on the limit values of the field in
can be determined based on the limit values of the field in ![]() and
and ![]() at this point. If
at this point. If ![]() is taken small, the curvature
of the field in
is taken small, the curvature
of the field in ![]() approaches a straight line. If
the direction of the field in
approaches a straight line. If
the direction of the field in ![]() is the opposite of the field
in
is the opposite of the field
in ![]() at the boundary
at the boundary ![]() , this point is stable.
In Fig. 11 this corresponds to the point on
, this point is stable.
In Fig. 11 this corresponds to the point on ![]() reached
by trajectory 3.
reached
by trajectory 3.
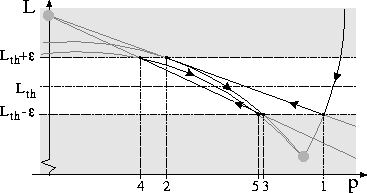
Figure 12: Iteration across hysteresis effect.