4 The Temporal Causal Graph

The bond graph model of the physical system is used to derive a temporal causal graph which captures the dynamic characteristics of system behavior. The temporal causal graph is derived in two steps [14, 18]:

1. The SCAP or its extended versions [23] are applied to generate a causal assignment among the power variables associated with the bond graph. These power variables are vertices in the temporal causal graph.
2. Components are linked one on one to individual edges in the temporal causal graph, and additional temporal and magnitude constraints are added to them.

In the diagnosis models that are used, bond graph elements operate in so-called integral causality only [21]. This results in a unique causal assigment of all components that embody temporal effects. As a result from resistive elements, which have indifferent causality, algebraic equations may be present in the system model. Causal assignment in these symmetric equations is not critical for deriving a consistent system description, and, therefore, the results of graph operations are the same, irrespective of the causal assigment.

The temporal causal graph for the bi-tank system in Fig. 4 is derived from the causally augmented bond graph in Fig. 5 and shown in Fig. 7. The graphical structure represents effort and flow variables as vertices, and relations between the variables as directed edges. The relations can be attributed to junctions and system components. Junction relations add labels -1, 1, and = to a graph edge. The = implies that the junction constrains the two variable vertices associated with the edge to take on equal values, 1 implies a direct proportionality and -1 implies an inverse proportionality for the variable associated with the two incident vertices. When the edge is associated with a component, it represents the component's constituent relation. For example, for a resistor with flow causality, the edge between effort and flow is labeled and for a capacitor the edge is labeled .

  
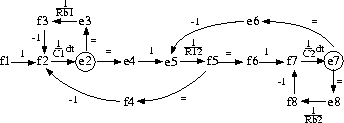
Figure 7: Temporal causal graph of the bi-tank system.

Junctions (0, 1), transformers (TF, GY), and resistors (R) introduce magnitude relations that are instantaneous, whereas capacitors (C) and inductors (I) also introduce temporal effects. In general, these temporal effects are integrating, and their associated rate of change is determined by the path that links an observed variable to the initial point where a deviation occurs. Note the natural feedback mechanisms of dynamic physical systems that result in closed paths in the temporal causal graph. Between passive elements, these feedback mechanisms always have a negative gain [24] and if they include an integrating effect, as a result from a state variable in the system, these closed paths are referred to as state loops.

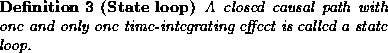
An added advantage of bond graph models is that they allow automatic derivation of the steady state model of the system. In case of the bi-tank system, both the tank capacities in steady state can be replaced by flow sources with value 0, since no change of stored energy takes place. The steady state bond graph and its resulting steady state causal graph are shown in Fig. 8. Notice that the causality links in the steady state graph differ from the causality links in the dynamic behavior graph (Fig. 7) and have less meaning. Since there is no unique causal ordering, a steady state graph represents a set of algebraic equations rather than differential equations. Causality helps solve these equations, but its actual assignment is not critical. Independent of causality assignment in steady state graphs, the set of algebraic equations is invariant and equal effects of parameter deviations are generated for different causality assignments.

  
Figure 8: Steady state bond graph of the bi-tank system and its corresponding causal graph.